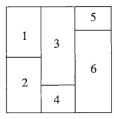
【題目】現用4種不同的顏色對如圖所示的正方形的6個區域進行涂色，要求相鄰的區域不能涂同一種顏色，則不同的涂色方案有______種.
【答案】144
【解析】
依次計算每個區域的涂色方法種數，然后利用分步乘法計數原理求解即可.
第一步，對區域1進行涂色，有4種顏色可供選擇，即有4種不同的涂色方法；
第二步，對區域2進行涂色，區域2與區域1相鄰，有3種顏色可供選擇，即有3種不同的涂色方法；
第三步，對區域3進行涂色，區域3與區域1、區域2相鄰，有2種顏色可供選擇，即有2種不同的涂色方法；
第四步，對于區域4進行涂色，區域4與區域2、區域3相鄰，有2種顏色可供選擇，即有2種不同的涂色方法；
第五步，對區域5進行涂色，若其顏色與區域4相同，則區域6有2種涂色方法，若其顏色與區域4不同，則區域6只有1種涂色方法，故區域5，6共有
種涂色方法，
由分步乘法計數原理知，不同的涂色方案的種數為
.
故答案為：144
閱讀快車系列答案科目：高中數學 來源： 題型：
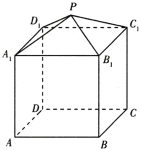
【題目】已知棱長為1的正方體
，過對角線
作平面
交棱
于點
，交棱
于點
，以下結論正確的是（ ）
A.四邊形
不一定是平行四邊形
B.平面分正方體所得兩部分的體積相等
C.平面與平面
不可能垂直
D.四邊形面積的最大值為
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是一個由正四棱錐
和正四棱柱
構成的組合體，正四棱錐的側棱長為6，
為正四棱錐高的4倍.當該組合體的體積最大時，點
到正四棱柱外接球表面的最小距離是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從0,1,2,3,4,5,6中取出三個不同的數字組成一個三位數，則這個三位數的各個位上的數字之和為奇數的取法共有_________種．（用數字作答）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知圓錐曲線
的參數方程為
（
為參數）．
（1）以原點為極點，
軸正半軸為極軸建立極坐標系，求圓錐曲線的極坐標方程；
（2）若直線l過曲線的焦點且傾斜角為60°，求直線l被圓錐曲線所截得的線段的長度．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，曲線C的參數方程為
(
為參數).以原點O為極點，x軸非負半軸為極軸建立極坐標系，直線l的極坐標方程為
.
（1）求曲線C的普通方程和直線l的直角坐標方程；
（2）點P是曲線C上的動點，求P到直線l的距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
為等邊三角形，邊長為2，
為等腰直角三角形，
，
，
，平面
平面ABCD.
(1)證明：
平面PAD；
(2)求平面PAD與平面PBC所成銳二面角的余弦值；
(3)棱PD上是否存在一點E，使得
平面PBC？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某居民區內有一直角梯形區域
，
，
，
百米，
百米.該區域內原有道路
，現新修一條直道
（寬度忽略不計），點
在道路上（異于
，
兩點），
，
.
（1）用
表示直道的長度；
（2）計劃在
區域內修建健身廣場，在
區域內種植花草.已知修建健身廣場的成本為每平方百米4萬元，種植花草的成本為每平方百米2萬元，新建道路的成本為每百米4萬元，求以上三項費用總和的最小值（單位：萬元）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
