
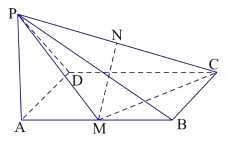
【題目】如圖,已知![]() 矩形
矩形![]() 所在的平面,
所在的平面, ![]() 分別為
分別為![]() 的中點,
的中點, ![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求![]() 與面
與面![]() 所成角大小的正弦值;
所成角大小的正弦值;
(3)求證: ![]() 面
面![]() .
.
【答案】(1)見解析(2)![]() (3)見解析
(3)見解析
【解析】試題分析:(1)取![]() 的中點
的中點![]() ,利用平幾知識證四邊形
,利用平幾知識證四邊形![]() 是平行四邊形.即得
是平行四邊形.即得![]() .再根據線面平行判定定理得
.再根據線面平行判定定理得![]() 平面
平面![]() ;(2)由
;(2)由![]() 矩形
矩形![]() 得
得![]() 即為
即為![]() 與面
與面![]() 所成角,再解直角三角形得
所成角,再解直角三角形得![]() 與面
與面![]() 所成角的正弦值(3)由等腰三角形性質得
所成角的正弦值(3)由等腰三角形性質得![]() ,再根據
,再根據![]() 矩形
矩形![]() 得
得![]() 而
而![]() ,所以根據線面垂直判定定理得
,所以根據線面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() ,因此
,因此![]() 平面
平面![]() .最后根據
.最后根據![]() ,得
,得![]() 面
面![]() .
.
試題解析:解:
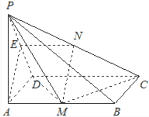
記![]() 中點為
中點為![]() ,易得
,易得![]() 平行且等于
平行且等于![]() ,
,
(1)證明:如圖,取![]() 的中點
的中點![]() ,連結
,連結![]() ,
,
則有![]() ,且
,且![]() ,
,
∴四邊形![]() 是平行四邊形.
是平行四邊形.
∴![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)易得![]() 即為
即為![]() 與面
與面![]() 所成角,
所成角, ![]() ,所以,
,所以, ![]() 與面
與面![]() 所成角大小的正弦值為
所成角大小的正弦值為![]() ;
;
(3)證明:∵![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() 為
為![]() 中點,
中點,
∴![]() ,又∵
,又∵![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩人練習罰球,每人練習6組,每組罰球20個,命中個數莖葉圖如下:
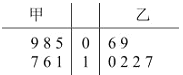
(1)求甲命中個數的中位數和乙命中個數的眾數;
(2)通過計算,比較甲乙兩人的罰球水平.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() ,
, ![]() .
.
(1)求證:對![]() ,直線
,直線![]() 與圓
與圓![]() 總有兩個不同的交點
總有兩個不同的交點![]() ;
;
(2)求弦![]() 的中點
的中點![]() 的軌跡方程,并說明其軌跡是什么曲線;
的軌跡方程,并說明其軌跡是什么曲線;
(3)是否存在實數![]() ,使得原
,使得原![]() 上有四點到直線
上有四點到直線![]() 的距離為
的距離為![]() ?若存在,求出
?若存在,求出![]() 的范圍;若不存在,說明理由.
的范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為自然對數的底數,
為自然對數的底數,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表達式;
的表達式;
⑵若![]() 時,方程
時,方程![]() 在
在![]() 上恰有兩個相異實根,求實根
上恰有兩個相異實根,求實根![]() 的取值范圍;
的取值范圍;
⑶若![]() ,
,![]() ,求使
,求使![]() 得圖像恒在
得圖像恒在![]() 圖像上方的最大正整數
圖像上方的最大正整數![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知矩形![]() 的對角線交于點
的對角線交于點![]() ,邊
,邊![]() 所在直線的方程為
所在直線的方程為![]() ,點
,點![]() 在邊
在邊![]() 所在的直線上.
所在的直線上.
(1)求矩形![]() 的外接圓的方程;
的外接圓的方程;
(2)已知直線![]() (
(![]() ),求證:直線
),求證:直線![]() 與矩形
與矩形![]() 的外接圓恒相交,并求出相交的弦長最短時的直線
的外接圓恒相交,并求出相交的弦長最短時的直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() ﹥
﹥![]() ﹥0)的離心率為
﹥0)的離心率為![]() ,短軸一個端點到右焦點的距離為
,短軸一個端點到右焦點的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,坐標原點
兩點,坐標原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,側面PAB⊥底面ABCD,底面ABCD為矩形,PA=PB,O為AB的中點,OD⊥PC.
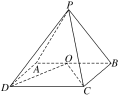
(1)求證:OC⊥PD;
(2)若PD與平面PAB所成的角為30°,求二面角DPCB的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】吉安一中舉行了一次“環保知識競賽”活動,為了解本了次競賽學生成績情況,從中抽取了部分學生的分數(得分取正整數,滿分為![]() 分)作為樣本(樣本容量為
分)作為樣本(樣本容量為![]() )進行統計.按照
)進行統計.按照 ![]() 的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出了得分在
的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出了得分在![]() 的數據).
的數據).
(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(2)在選取的樣本中,從競賽學生成績是![]() 分以上(含
分以上(含![]() 分)的同學中隨機抽取
分)的同學中隨機抽取![]() 名同學到市政廣場參加環保知識宣傳的志愿者活動,求所抽取的
名同學到市政廣場參加環保知識宣傳的志愿者活動,求所抽取的![]() 名同學中得分在
名同學中得分在![]() 的學生人數恰有一人的概率.
的學生人數恰有一人的概率.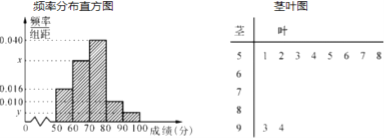
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com