
【題目】如圖,有一壁畫,最高點A處離地面AO=4m,最低點B處離地面BO=2m,觀賞它的C點在過墻角O點與地面成30°角的射線上. 
(1)設點C到墻的距離為x,當x= ![]() m時,求tanθ的值;
m時,求tanθ的值;
(2)問C點離墻多遠時,視角θ最大?
科目:高中數學 來源: 題型:
【題目】二項式![]() 的展開式中只有第6項的二項式系數最大,且展開式中的第3項的系數是第4項的系數的3倍,則
的展開式中只有第6項的二項式系數最大,且展開式中的第3項的系數是第4項的系數的3倍,則![]() 的值為( )
的值為( )
A. 4 B. 8 C. 12 D. 16
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(18)(本小題滿分12分)在心理學研究中,常采用對比試驗的方法評價不同心理暗示對人的影響,具體方法如下:將參加試驗的志愿者隨機分成兩組,一組接受甲種心理暗示,另一組接受乙中心理暗示,通過對比這兩組志愿者接受心理暗示后的結果來評價兩種心理暗示的作用,現有6名男志愿者A1,A2,A3,A4,A5,A6和4名B1,B2,
B3,B4,從中隨機抽取5人接受甲種心理暗示,另5人接受乙種心理暗示。
(I)求接受甲種心理暗示的志愿者中包含A1但不包含B3的頻率。
(II)用X表示接受乙種心理暗示的女志愿者人數,求X的分布列與數學期望EX。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知極坐標系的極點與直角坐標系的原點重合,極軸與直角坐標系中![]() 軸的正半軸重合.若曲線
軸的正半軸重合.若曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 的參數方程化為極坐標方程;
的參數方程化為極坐標方程;
(2)由直線![]() 上一點向曲線
上一點向曲線![]() 引切線,求切線長的最小值.
引切線,求切線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}的前n項和Sn=2n+r.
(1)求實數r的值和{an}的通項公式;
(2)若數列{bn}滿足b1=1,bn+1﹣bn=log2an+1 , 求bn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在多面體![]() 中,
中, ![]() 與
與![]() 均為邊長為2的正方形,
均為邊長為2的正方形, ![]() 為等腰直角三角形,
為等腰直角三角形, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出x與銷售額(單位:百萬元)之間有如下對應數據:
如果y與x之間具有線性相關關系.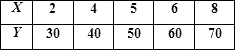
(1)作出這些數據的散點圖;
(2)求這些數據的線性回歸方程;
(3)預測當廣告費支出為9百萬元時的銷售額.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com