【題目】如圖所示，已知AB丄平面BCD，M、N分別是AC、AD的中點，BC 丄 CD.
（1）求證：MN//平面BCD；
（2）若AB=1，BC=
，求直線AC與平面BCD所成的角.
科目：高中數學 來源： 題型：
【題目】學校藝術節對同一類的
， 
， 
， 
四項參賽作品，只評一項一等獎，在評獎揭曉前，甲、乙、丙、丁四位同學對這四項參賽作品獲獎情況預測如下：
甲說：“
或
作品獲得一等獎”
乙說：“
作品獲得一等獎”
丙說：“
， 
兩項作品未獲得一等獎”
丁說：“
作品獲得一等獎”．
若這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知A，B分別是直線y=x和y=﹣x上的兩個動點，線段AB的長為2 
，D是AB的中點．
（1）求動點D的軌跡C的方程；
（2）若過點（1，0）的直線l與曲線C交于不同兩點P、Q，
①當|PQ|=3時，求直線l的方程；
②試問在x軸上是否存在點E（m，0），使 
恒為定值？若存在，求出E點的坐標及定值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}中，an=32，sn=63，
（1）若數列{an}為公差為11的等差數列，求a1；
（2）若數列{an}為以a1=1為首項的等比數列，求數列{am2}的前m項和sm′ ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】運貨卡車以每小時x千米的速度勻速行駛130千米（50≤x≤100）（單位：千米/小時）．假設汽油的價格是每升2元，而汽車每小時耗油（2+ 
）升，司機的工資是每小時14元．
（1）求這次行車總費用y關于x的表達式；
（2）當x為何值時，這次行車的總費用最低，并求出最低費用的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形
中， 
， 
， 
， 
， 
分別在
上， 
，現將四邊形
沿
折起，使
.
（1）若
，在折疊后的線段
上是否存在一點
，使得
平面
？若存在，求出
的值；若不存在，說明理由；
（2）求三棱錐
的體積的最大值，并求出此時點
到平面
的距離.
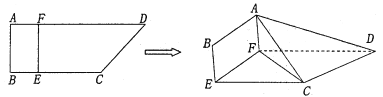
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點P（x、y）滿足
（1）若x∈{0，1，2，3，4，5}，y∈{0，1，2，3，4}，則求y≥x的概率．
（2）若x∈[0，5]，y∈[0，4]，則求x＞y的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在多面體
中，底面
是邊長為
的菱形， 
，四邊形
是矩形，平面
平面
， 
， 
是
的中點.
（1）求證： 
平面
；
（2）求直線
與平面
所成角的正弦值；
（3）求二面角
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
