【題目】已知函數
，曲線
在點
處的切線方程為
(1) 求
的值；
(2) 證明: 
.
【答案】（1）
；（2）見解析
【解析】分析：第一問結合導數的幾何意義以及切點在切線上也在函數圖像上，從而建立關于
的等量關系式，從而求得結果；第二問可以有兩種方法，一是將不等式轉化，構造新函數，利用導數研究函數的最值，從而求得結果，二是利用中間量來完成，這樣利用不等式的傳遞性來完成，再者這種方法可以簡化運算.
詳解：（1）解：
，由題意有
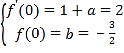，解得
（2）證明：（方法一）由（1）知，
.設
則只需證明
，設
則
， 
在
上單調遞增
，
，使得
且當
時，
，當
時，
當時，
，
單調遞減
當時，
，單調遞增
，由
，得
，
，
設
，
，
當時，
，
在
單調遞減，
，因此
（方法二）先證當
時， 
，即證
設
，則
，且
，
在
單調遞增，
在單調遞增，則當時，
（也可直接分析
顯然成立）
再證
設
，則
，令
，得
且當
時，，單調遞減；
當
時，，單調遞增.
，即
又
，
每課必練系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
(a>b>0)的一個頂點為A(2,0)，離心率為
.直線y＝k(x－1)與橢圓C交于不同的兩點M，N.
(1)求橢圓C的方程；
(2)當△AMN的面積為
時，求k的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某公司舉行的年終慶典活動中，主持人利用隨機抽獎軟件進行抽獎：由電腦隨機生成一張如圖所示的3
3表格，其中1格設獎300元，4格各設獎200元，其余4格各設獎100元，點擊某一格即顯示相應金額．某人在一張表中隨機不重復地點擊3格，記中獎的總金額為X元．
（1）求概率
；
（2）求
的概率分布及數學期望
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓C：
的離心率為
，其右焦點到橢圓C外一點
的距離為
，不過原點O的直線l與橢圓C相交于A，B兩點，且線段AB的長度為2．
1
求橢圓C的方程；
2求
面積S的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
