
【題目】如圖,∠C= ![]() ,AC=BC,M、N分別是BC、AB的中點,將△BMN沿直線MN折起,使二面角B′﹣MN﹣B的大小為
,AC=BC,M、N分別是BC、AB的中點,將△BMN沿直線MN折起,使二面角B′﹣MN﹣B的大小為 ![]() ,則B'N與平面ABC所成角的正切值是( )
,則B'N與平面ABC所成角的正切值是( ) 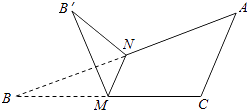
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵∠C= ![]() ,AC=BC,M、N分別是BC、AB的中點,將△BMN沿直線MN折起,使二面角B′﹣MN﹣B的大小為
,AC=BC,M、N分別是BC、AB的中點,將△BMN沿直線MN折起,使二面角B′﹣MN﹣B的大小為 ![]() ,
,
∴∠BMB′= ![]() ,
,
取BM的中點D,連B′D,ND,
由于折疊之前BM與CM都始終垂直于MN,這在折疊之后仍然成立,
∴折疊之后平面B′MN與平面BMN所成的二面角即為∠B′MD=60°,
并且B′在底面ACB內的投影點D就在BC上,且恰在BM的中點位置,
∴B′D⊥BC,B′D⊥AD,B′D⊥面ABC,
∴∠B′ND就為斜線B′N與平面ABC所成的角
設AC=BC=a,則B′D= ![]() ,B′N=
,B′N= ![]() ,DN=
,DN= ![]()
![]() ,
,
tan∠B′ND= ![]() =
= ![]() =
= ![]() .
.
故B'N與平面ABC所成角的正切值是 ![]() .
.
故選:D.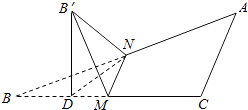
【考點精析】認真審題,首先需要了解空間角的異面直線所成的角(已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則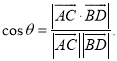 ).
).


科目:高中數學 來源: 題型:
【題目】隨著我國經濟的發展,居民的儲蓄存款逐年增長.設某地區城鄉居民人民幣儲蓄存款(年底余額)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
時間代號t | 1 | 2 | 3 | 4 | 5 |
儲蓄存款y(千億元) | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y關于t的回歸方程 ![]() =
= ![]() t+
t+ ![]() .
.
(Ⅱ)用所求回歸方程預測該地區2015年(t=6)的人民幣儲蓄存款.
附:回歸方程 ![]() =
= ![]() t+
t+ ![]() 中
中 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數y=f(x)的圖象上每一點的縱坐標保持不變,橫坐標伸長到原來的2倍,再將整個圖象沿x軸向右平移 ![]() 個單位,沿y軸向下平移1個單位,得到函數y=
個單位,沿y軸向下平移1個單位,得到函數y= ![]() sinx的圖象,則y=f(x)的解析式為( )
sinx的圖象,則y=f(x)的解析式為( )
A.y= ![]() sin(2x+
sin(2x+ ![]() )+1
)+1
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1
)+1
C.y= ![]() sin(
sin( ![]() x+
x+ ![]() )+1
)+1
D.y= ![]() sin(
sin( ![]() x﹣
x﹣ ![]() )+1
)+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】Sn為等差數列{an}的前n項和,且a1=1,S7=28,記bn=[lgan],其中[x]表示不超過x的最大整數,如[0.9]=0,[lg99]=1. (Ⅰ)求b1 , b11 , b101;
(Ⅱ)求數列{bn}的前1000項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sinx,將函數y=f(x)的圖象向右平移![]() 個單位,再把橫坐標縮短到原來的
個單位,再把橫坐標縮短到原來的![]() (縱坐標不變),得到函數y=g(x)的圖象,求函數y=g(x)的解析式,并寫出它的單調遞增區間.
(縱坐標不變),得到函數y=g(x)的圖象,求函數y=g(x)的解析式,并寫出它的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將A,B兩枚骰子各拋擲一次,觀察向上的點數,問:
(1)共有多少種不同的結果?
(2)兩枚骰子點數之和是3的倍數的結果有多少種?
(3)兩枚骰子點數之和是3的倍數的概率為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD= ![]() ,O為AC與BD的交點,E為棱PB上一點.
,O為AC與BD的交點,E為棱PB上一點.
(Ⅰ)證明:平面EAC⊥平面PBD;
(Ⅱ)若PD∥平面EAC,求三棱錐P﹣EAD的體積.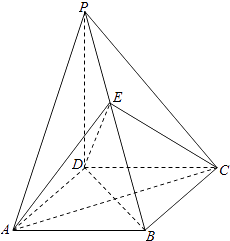
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論中,正確的是( )
A.冪函數的圖象都通過點(0,0),(1,1)
B.冪函數的圖象可以出現在第四象限
C.當冪指數α取1,3, ![]() 時,冪函數y=xα是增函數
時,冪函數y=xα是增函數
D.當冪指數α=-1時,冪函數y=xα在定義域上是減函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的三內角A、B、C成等差數列,sinA、sinB、sinC成等比數列,則這個三角形的形狀是( )
A.直角三角形
B.鈍角三角形
C.等腰直角三角形
D.等邊三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com