
【題目】已知![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為軸將
為軸將![]() 旋轉
旋轉![]() 到
到![]() ,形成三棱錐
,形成三棱錐![]() .
.
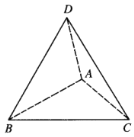
(Ⅰ)求證:![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(Ⅰ)詳見解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,取
,取![]() 的中點
的中點![]() 及
及![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,![]() .證明
.證明![]() 平面
平面![]() ,即得
,即得![]() ,再由平面幾何知識得
,再由平面幾何知識得![]() ,由
,由![]() 可得線面垂直,從而得證線線垂直;
可得線面垂直,從而得證線線垂直;
(Ⅱ)作出直線與平面所成的角,通過解三角形求解.
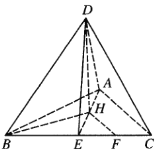
(Ⅰ)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,取
,取![]() 的中點
的中點![]() 及
及![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,![]() .則
.則![]() ,
,
∵![]() ,∴
,∴![]() ,由旋轉知
,由旋轉知![]() ,
,
∴二面角![]() 的平面角即為
的平面角即為![]() ,
,
且![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
∵![]() ,
,![]() ,
,
∴![]() 為正三角形,∴
為正三角形,∴![]() .
.
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
易求得![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,![]() ,則
,則![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,從而
,從而![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ∴
∴![]() .
.
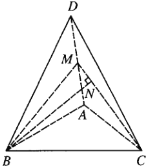
(Ⅱ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() 邊上的高,垂足為
邊上的高,垂足為![]() .
.
∵![]() ,又
,又![]() ,且
,且![]() 為
為![]() 的中點,
的中點,
∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴直線![]() 與平面
與平面![]() 所成的角即為
所成的角即為![]() ,
,
由(Ⅰ)可知![]() 為正三角形,可知
為正三角形,可知![]() ,
,
則易求得![]() ,
,![]() ,
,
∴![]() ,則
,則![]() ,
,
即直線![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】2020年是全面建成小康社會目標實現之年,也是全面打贏脫貧攻堅戰收官之年.某鄉鎮在2014年通過精準識別確定建檔立卡的貧困戶共有500戶,結合當地實際情況采取多項精準扶貧措施,每年新脫貧戶數如下表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代碼 | 1 | 2 | 3 | 4 | 5 |
脫貧戶數 | 55 | 68 | 80 | 92 | 100 |
(1)根據2015-2019年的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測到2020年底該鄉鎮500戶貧困戶是否能全部脫貧;
,并預測到2020年底該鄉鎮500戶貧困戶是否能全部脫貧;
(2)2019年的新脫貧戶中有20戶五保戶,20戶低保戶,60戶扶貧戶.該鄉鎮某干部打算按照分層抽樣的方法對2019年新脫貧戶中的5戶進行回訪,了解生產生活、幫扶工作開展情況.為防止這些脫貧戶再度返貧,隨機抽取這5戶中的2戶進行每月跟蹤幫扶,求抽取的2戶不都是扶貧戶的概率.
參考公式: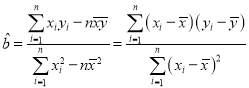 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=ex﹣ax2﹣ax,h(x)=ex﹣2x﹣lnx.其中e為自然對數的底數.
(1)若f(x)=h(x)﹣g(x).
①討論f(x)的單調性;
②若函數f(x)有兩個不同的零點,求實數a的取值范圍.
(2)已知a>0,函數g(x)恰有兩個不同的極值點x1,x2,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 為拋物線上一點(
為拋物線上一點(![]() 在
在![]() 軸上方),
軸上方),![]() ,
,![]() 點到
點到![]() 軸的距離為4.
軸的距離為4.
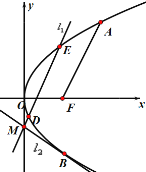
(1)求拋物線方程及點![]() 的坐標;
的坐標;
(2)是否存在![]() 軸上的一個點
軸上的一個點![]() ,過點
,過點![]() 有兩條直線
有兩條直線![]() ,滿足
,滿足![]() ,
,![]() 交拋物線
交拋物線![]() 于
于![]() 兩點.
兩點.![]() 與拋物線相切于點
與拋物線相切于點![]() (
(![]() 不為坐標原點),有
不為坐標原點),有![]() 成立,若存在,求出點
成立,若存在,求出點![]() 的坐標.若不存在,請說明理由.
的坐標.若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某個微信群某次進行的搶紅包活動中,群主所發紅包的總金額為10元,被隨機分配為2.49元、1.32元、2.19元、0.63元、3.37元共5份,供甲、乙等5人搶,每人只能搶一次,則甲、乙二人搶到的金額之和不低于4元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】著名數學家華羅庚先生曾說過:“數缺形時少直觀,形缺數時難入微數形結合百般好,隔裂分家萬事休.”在數學的學習和研究中,我們經常用函數的圖象來研究函數的性質,也經常用函數的解析式來琢磨函數的圖象的特征,如某體育品牌的LOGO為![]() ,可抽象為如圖所示的軸對稱的優美曲線,下列函數中,其圖象大致可“完美”局部表達這條曲線的函數是( )
,可抽象為如圖所示的軸對稱的優美曲線,下列函數中,其圖象大致可“完美”局部表達這條曲線的函數是( )
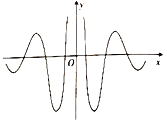
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com