
【題目】已知函數![]() .
.
(1)討論![]() 的極值點的個數;
的極值點的個數;
(2)當![]() 時,若存在實數
時,若存在實數![]() ,使得
,使得![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)先求得函數![]() 的導函數
的導函數![]() .令
.令![]() ,分離參數后構造函數
,分離參數后構造函數![]() ,并求得
,并求得![]() ,通過判斷
,通過判斷![]() 在各區間內的符號,判斷
在各區間內的符號,判斷![]() 的單調性及
的單調性及![]() 的取值情況.即可根據
的取值情況.即可根據![]() 的取值情況,判斷極值點的個數.
的取值情況,判斷極值點的個數.
(2)將![]() 代入,并令
代入,并令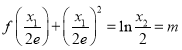 ,即可用
,即可用![]() 表示出
表示出![]() 與
與![]() ,即可表示出
,即可表示出![]() .構造函數
.構造函數![]() ,并求得
,并求得![]() ,結合
,結合![]() 的符號即可判斷
的符號即可判斷![]() 的單調性,進而求得
的單調性,進而求得![]() 的最小值.
的最小值.
(1)由題可知![]() ,
,
令![]() ,得
,得![]() ,
,
記![]() ,則
,則![]()
當![]() 時,
時,![]() ;
;![]() 時,
時,![]() ;
;![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
又![]()
![]() 時,
時,![]() ;
;
![]() 時,
時,![]() ;
;
![]() 時,
時,![]() ,
,
∴當![]() 時,函數
時,函數![]() 有2個極值點;
有2個極值點;
當![]() 時,函數
時,函數![]() 無極值點;
無極值點;
當![]() 時,函數
時,函數![]() 有1個極值點;
有1個極值點;
(2)當![]() 時,設
時,設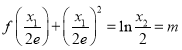 ,
,
則![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
故![]() ,
,![]() ,
,
∴![]() ,
,![]() ,即
,即![]() .
.
令![]() ,
,
則![]() ,
,
∵![]() 與
與![]() 在
在![]() 均單調遞增,
均單調遞增,
∴![]() 在
在![]() 均單調遞增,且
均單調遞增,且![]() ,
,
∴當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴當![]() 時,
時,![]() 取最小值,此時
取最小值,此時![]() ,
,
即![]() 的最小值為
的最小值為![]() .
.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() :
:![]() (
(![]() 為參數),曲線
為參數),曲線![]() :
: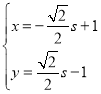 (
(![]() 為參數),以O為極點,
為參數),以O為極點,![]() 軸的非負半軸為極軸的極坐標系中,已知曲線
軸的非負半軸為極軸的極坐標系中,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,記曲線
,記曲線![]() 與
與![]() 的交點為
的交點為![]() .
.
(1)求點![]() 的極坐標;
的極坐標;
(2)設曲線![]() 與
與![]() 相交于A,B兩點,求
相交于A,B兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 有極值,且導函數
有極值,且導函數![]() 的極值點是
的極值點是![]() 的零點,給出命題:①
的零點,給出命題:①![]() ;②若
;②若![]() ,則存在
,則存在![]() ,使得
,使得![]() ;③
;③![]() 與
與![]() 所有極值之和一定小于0;④若
所有極值之和一定小于0;④若![]() ,且
,且![]() 是曲線
是曲線![]() 的一條切線,則
的一條切線,則![]() 的取值范圍是
的取值范圍是![]() .則以上命題正確序號是_____________.
.則以上命題正確序號是_____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在實數
,若存在實數![]() ,使
,使![]() 成立,則稱
成立,則稱![]() 為
為![]() 的不動點.
的不動點.
(1)當![]() ,
,![]() 時,求
時,求![]() 的不動點;
的不動點;
(2)若對于任何實數![]() ,函數
,函數![]() 恒有兩相異的不動點,求實數
恒有兩相異的不動點,求實數![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若![]() 的圖象上
的圖象上![]() 、
、![]() 兩點的橫坐標是函數
兩點的橫坐標是函數![]() 的不動點,且直線
的不動點,且直線![]() 是線段
是線段![]() 的垂直平分線,求實數
的垂直平分線,求實數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】世界排球比賽一般實行“五局三勝制”,在2019年第13屆世界女排俱樂部錦標賽(俗稱世俱杯)中,中國女排和某國女排相遇,根據歷年數據統計可知,在中國女排和該國女排的比賽中,每場比賽中國女排獲勝的概率為![]() ,該國女排獲勝的概率為
,該國女排獲勝的概率為![]() ,現中國女排在先勝一局的情況下獲勝的概率為( )
,現中國女排在先勝一局的情況下獲勝的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 與
與![]() 的交點坐標;
的交點坐標;
(2)過曲線![]() 上任一點
上任一點![]() 作與
作與![]() 夾角為30°的直線,交
夾角為30°的直線,交![]() 于點
于點![]() ,且
,且![]() 的最大值為
的最大值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知A,B分別為橢圓C:![]() (a>b>0)的左右頂點,P為橢圓C上異于A,B的任意一點,O為坐標原點,
(a>b>0)的左右頂點,P為橢圓C上異于A,B的任意一點,O為坐標原點,![]()
![]() =﹣4,△PAB的面積的最大值為
=﹣4,△PAB的面積的最大值為![]() .
.
(1)求橢圓C的方程;
(2)若橢圓C上存在兩點M,N,分別滿足OM∥PA,ON∥PB,求|OM||ON|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,直線l與橢圓C交于P,Q兩點,且點M滿足
,直線l與橢圓C交于P,Q兩點,且點M滿足![]() .
.
(1)若點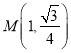 ,求直線
,求直線![]() 的方程;
的方程;
(2)若直線l過點![]() 且不與x軸重合,過點M作垂直于l的直線
且不與x軸重合,過點M作垂直于l的直線![]() 與y軸交于點
與y軸交于點![]() ,求實數t的取值范圍.
,求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com