【題目】在平面直角坐標系xoy中，以O為極點，x軸的正半軸為極軸的極坐標系中，直線l的極坐標方程為θ= 
，曲線C的參數(shù)方程為 
．
（1）寫出直線l與曲線C的直角坐標方程；
（2）過點M平行于直線l1的直線與曲線C交于A、B兩點，若|MA||MB|= 
，求點M軌跡的直角坐標方程．
【答案】
（1）解：直線l的極坐標方程為θ= 
，所以直線斜率為1，直線l：y=x；
曲線C的參數(shù)方程為 
．消去參數(shù)θ，
可得曲線 
（2）解：設點M（x0，y0）及過點M的直線為 
由直線l1與曲線C相交可得： 
，即： 
，
x2+2y2=6表示一橢圓
取y=x+m代入 
得：3x2+4mx+2m2﹣2=0
由△≥0得 
故點M的軌跡是橢圓x2+2y2=6夾在平行直線 
之間的兩段弧
【解析】（1）利用極坐標與直角坐標方程的互化，直接寫出直線l的普通方程，消去參數(shù)可得曲線C的直角坐標方程；（2）設點M（x0 ， y0）以及平行于直線l1的直線參數(shù)方程，直線l1與曲線C聯(lián)立方程組，通過|MA||MB|= 
，即可求點M軌跡的直角坐標方程．通過兩個交點推出軌跡方程的范圍，
科目：高中數(shù)學 來源： 題型：
【題目】若ABC的三個頂點的坐標分別為A（4，0），B（6，7），C（0，3）．
①求BC邊上的高所在直線的方程；
②求BC邊上的中線所在的直線方程．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，A（a，0）（a＞0），B（0，a），C（﹣4，0），D（0，4）設△AOB的外接圓圓心為E．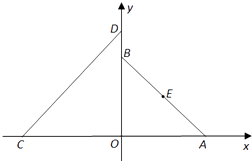 
（1）若⊙E與直線CD相切，求實數(shù)a的值；
（2）設點P在圓E上，使△PCD的面積等于12的點P有且只有三個，試問這樣的⊙E是否存在，若存在，求出⊙E的標準方程；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，已知四棱錐的側棱PD⊥底面ABCD，且底面ABCD是直角梯形，AD⊥CD，AB∥CD，AB=AD= 
CD=2，點M在側棱上．
（1）求證：BC⊥平面BDP；
（2）若側棱PC與底面ABCD所成角的正切值為 ，點M為側棱PC的中點，求異面直線BM與PA所成角的余弦值．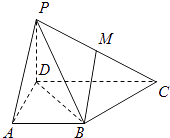 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù) 
，g（x）=xlnx﹣a（x﹣1）．
（1）求函數(shù)f（x）在點（4，f（4））處的切線方程；
（2）若對任意x∈（0，+∞），不等式g（x）≥0恒成立，求實數(shù)a的取值的集合M；
（3）當a∈M時，討論函數(shù)h（x）=f（x）﹣g（x）的單調性．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖所示，A，B兩點5條連線并聯(lián)，它們在單位時間內能通過的最大信息量依次為2，3，4，3，2．現(xiàn)記從中任取三條線且在單位時間內都通過的最大信息總量為ξ，則P（ξ≥8）= ．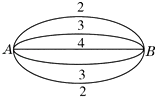 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】中國古代數(shù)學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗，苗主責之粟五斗，羊主曰:“我羊食半馬.”馬主曰:“我馬食半牛.”今欲衰償之，問各出幾何？此問題的譯文是:今有牛、馬、羊吃了別人的禾苗，禾苗主人要求賠償5斗粟.羊主人說:“我羊所吃的禾苗只有馬的一半.”馬主人說:“我馬所吃的禾苗只有牛的一半.”打算按此比例償還，他們各應償還多少？已知牛、馬、羊的主人各應償還
升， 
升， 
升，1斗為10升，則下列判斷正確的是( )
A. 
， 
， 
依次成公比為2的等比數(shù)列，且
B. 
， 
， 
依次成公比為2的等比數(shù)列，且
C. 
， 
， 
依次成公比為
的等比數(shù)列，且
D. 
， 
， 
依次成公比為
的等比數(shù)列，且
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】（選修4﹣5：不等式選講）
已知函數(shù)f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．
（1）當a=﹣2時，求不等式f（x）＜g（x）的解集；
（2）設a＞﹣1，且當 
時，f（x）≤g（x），求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
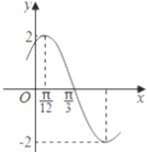
【題目】已知函數(shù)
的部分圖象如圖所示．
（Ⅰ）求函數(shù)
的解析式；
（Ⅱ）將函數(shù)
的圖象做怎樣的平移變換可以得到函數(shù)
的圖象；
（Ⅲ）若方程
在
上有兩個不相等的實數(shù)根，求
的取值范圍．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com