Question

【題目】已知函數f（x）=ax﹣（a+1）ln（x+1），其中a＞0．
（1）求f（x）的單調區間；
（2）設f（x）的最小值為g（a），求證： ．

Answer 1

【答案】
（1）解：由已知可得函數f（x）的定義域為（﹣1，+∞），

而 ，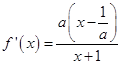

∵a＞0，x＞﹣1，∴當 時，f'（x）＜0，

當 時，f'（x）＞0，

∴函數f（x）的單調遞減區間是 ，單調遞增區間是

（2）解：由（1）可知，f（x）的最小值

為 ，a＞0．

要證明 ，

只須證明 成立．

設 ，x∈（0，+∞）．

則 ，

∴φ（x）在區間（0，+∞）上是增函數，∴φ（x）＞φ（0）=0，即 ．

取 得到 成立．

設ψ（x）=ln（x+1）﹣x，x∈（0，+∞），同理可證ln（x+1）＜x．

取 得到 成立．因此，

【解析】（1）先對函數進行求導，根據導函數大于0原函數單調遞增，導函數小于0原函數單調遞減可得答案；（2）由（1）可知，f（x）的最小值為 ，a＞0，構造函數設 ，x∈（0，+∞），利用導數研究函數的單調性和最值，即可證明結論．
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的最大(小)值與導數，需要了解一般的,函數的單調性與其導數的正負有如下關系： 在某個區間內，(1)如果，那么函數在這個區間單調遞增；(2)如果，那么函數在這個區間單調遞減；求函數在上的最大值與最小值的步驟：（1）求函數在內的極值；（2）將函數的各極值與端點處的函數值，比較，其中最大的是一個最大值，最小的是最小值才能得出正確答案．