【題目】過點
的動直線l與y軸交于點
，過點T且垂直于l的直線
與直線
相交于點M.
（1）求M的軌跡方程；
（2）設(shè)M位于第一象限，以AM為直徑的圓
與y軸相交于點N，且
，求
的值.
【答案】（1）
（2）4
【解析】
（1）動直線l過點
和
，可根據(jù)垂直求出直線
，從而求出交點M的坐標(biāo)，從而尋找橫縱坐標(biāo)的關(guān)系，求出點M的軌跡方程. （2）由題意可知：點N即為圓與y軸的切點，根據(jù)
，可求出直線AM的斜率，進而求出直線AM的方程，從而求出
的值.
解：（1）∵，，當(dāng)
時，M的坐標(biāo)為
當(dāng)
時，
，∴
，∴的方程為
由
得
，
驗證當(dāng)時，也滿足
∴M的坐標(biāo)滿足方程，即M的軌跡方程為
（2）作
軸于
，
軸于
，則
又A為拋物線的焦點，∴
，故圓
與y軸相切于點N
∵，∵
，∴
，∴直線AM的方程為
聯(lián)立
，消去y整理得
，解得
或
（舍），即
∵A為拋物線的焦點，∴
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列{an}滿足a1＝1，an＝
(n∈N*，n≥2)，數(shù)列{bn}滿足關(guān)系式bn＝
(n∈N*)．
(1)求證：數(shù)列{bn}為等差數(shù)列；
(2)求數(shù)列{an}的通項公式．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，以原點
為極點，
軸正半軸為極軸建立極坐標(biāo)系．已知直線
的極坐標(biāo)方程為
，曲線
的極坐標(biāo)方程為
．
（1）寫出直線和曲線的直角坐標(biāo)方程；
（2）過動點
且平行于的直線交曲線于
兩點，若
，求動點
到直線的最近距離．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
，點
，
，
分別為橢圓的左焦點、右頂點和下頂點，
的面積為
，且橢圓的離心率為
.
（1）求橢圓的標(biāo)準(zhǔn)方程；
（2）若點
為橢圓
上一點，直線
與橢圓交于不同的兩點
，
，且
（點
為坐標(biāo)原點），求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
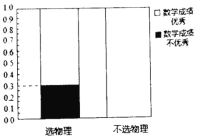
【題目】某省即將實行新高考，不再實行文理分科.某校為了研究數(shù)學(xué)成績優(yōu)秀是否對選擇物理有影響，對該校2018級的1000名學(xué)生進行調(diào)查，收集到相關(guān)數(shù)據(jù)如下：
（1）根據(jù)以上提供的信息，完成
列聯(lián)表，并完善等高條形圖；
選物理 | 不選物理 | 總計 | |
數(shù)學(xué)成績優(yōu)秀 | |||
數(shù)學(xué)成績不優(yōu)秀 | 260 | ||
總計 | 600 | 1000 |
（2）能否在犯錯誤的概率不超過0.05的前提下認為數(shù)學(xué)成績優(yōu)秀與選物理有關(guān)？
附：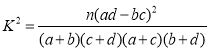
臨界值表：
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
，
，
，給出以下四個命題：①
為偶函數(shù)；②
為偶函數(shù)；③的最小值為0；④有兩個零點．其中真命題的是（ ）．
A.②④B.①③C.①③④D.①④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，直線
的參數(shù)方程為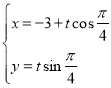
（
為參數(shù)），以坐標(biāo)原點
為極點，
軸正半軸為極軸建立極坐標(biāo)系，曲線
的極坐標(biāo)方程為
.
（Ⅰ）求直線的普通方程及曲線的直角坐標(biāo)方程；
（Ⅱ）已知點
是曲線上的任意一點，當(dāng)點到直線的距離最大時，求經(jīng)過點且與直線平行的直線
的方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
．
（1）設(shè)兩點
，
，且
，若函數(shù)
的圖象分別在點
、
處的兩條切線互相垂直，求
的最小值；
（2）若對任意
，
恒成立，求實數(shù)
的取值范圍．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
