
【題目】給出下列四個命題:
①![]() 中,
中,![]() 是
是![]() 成立的充要條件;
成立的充要條件;
②當![]() 時,有
時,有![]() ;
;
③已知![]() 是等差數列
是等差數列![]() 的前n項和,若
的前n項和,若![]() ,則
,則![]() ;
;
④若函數![]() 為
為![]() 上的奇函數,則函數
上的奇函數,則函數![]() 的圖象一定關于點
的圖象一定關于點![]() 成中心對稱.其中所有正確命題的序號為___________.
成中心對稱.其中所有正確命題的序號為___________.
【答案】①③
【解析】
①利用正弦定理可判斷;②舉反例即可判斷;③利用等差數列等差中項計算可判斷;
④根據奇函數的性質與函數圖象平移可判斷.
①在△ABC中,由正弦定理可得 ![]() , ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要條件,①正確;
, ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要條件,①正確;
②當1>x>0時,lnx<0,所以不一定大于等于2,②不成立;
③等差數列{an}的前n項和,若S7>S5,則S7-S5=a6+a7>0,S9-S3=a4+a5+…+a9=3(a6+a7)>0,因此S9>S3,③正確;
④若函數![]() 為R上的奇函數,則其圖象關于(0,0)中心對稱,而函數y=f(x)的圖象是把y=f(x-
為R上的奇函數,則其圖象關于(0,0)中心對稱,而函數y=f(x)的圖象是把y=f(x-![]() )的圖象向左平移
)的圖象向左平移![]() 個單位得到的,故函數y=f(x)的圖象一定關于點F(-
個單位得到的,故函數y=f(x)的圖象一定關于點F(-![]() ,0)成中心對稱,④不正確.
,0)成中心對稱,④不正確.
綜上只有①③正確.


科目:高中數學 來源: 題型:
【題目】某校為研究學生語言學科的學習情況,現對高二200名學生英語和語文某次考試成績進行抽樣分析.將200名學生編號為001,002,…,200,采用系統抽樣的方法等距抽取10名學生,將10名學生的兩科成績(單位:分)繪成折線圖如下:
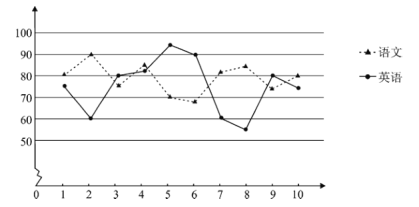
(1)若第二段抽取的學生編號是026,寫出第六段抽取的學生編號;
(2)在這兩科成績差低于20分的學生中隨機抽取2人進行訪談,求2人成績均是語文成績高于英語成績的概率;
(3)根據折線圖,比較該校高二年級學生的語文和英語兩科成績,寫出至少兩條統計結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
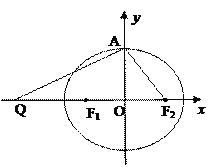
【題目】如圖,設橢圓![]() 的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且
的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且![]() 0,若過 A,Q,F2三點的圓恰好與直線
0,若過 A,Q,F2三點的圓恰好與直線![]() 相切,過定點 M(0,2)的直線
相切,過定點 M(0,2)的直線![]() 與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線
與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線![]() 的斜率
的斜率![]() ,在x軸上是否存在點P(
,在x軸上是否存在點P(![]() ,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出
,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數
的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數![]() 滿足
滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古印度“漢諾塔問題”:一塊黃銅平板上裝著![]() 三根金銅石細柱,其中細柱
三根金銅石細柱,其中細柱![]() 上套著個大小不等的環形金盤,大的在下、小的在上.將這些盤子全部轉移到另一根柱子上,移動規則如下:一次只能將一個金盤從一根柱子轉移到另外一根柱子上,不允許將較大盤子放在較小盤子上面.若
上套著個大小不等的環形金盤,大的在下、小的在上.將這些盤子全部轉移到另一根柱子上,移動規則如下:一次只能將一個金盤從一根柱子轉移到另外一根柱子上,不允許將較大盤子放在較小盤子上面.若![]() 柱上現有
柱上現有![]() 個金盤(如圖),將
個金盤(如圖),將![]() 柱上的金盤全部移到
柱上的金盤全部移到![]() 柱上,至少需要移動次數為( )
柱上,至少需要移動次數為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程。
已知曲線C![]() :
:![]() (t為參數), C
(t為參數), C![]() :
:![]() (
(![]() 為參數)。
為參數)。
(1)化C![]() ,C
,C![]() 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)若C![]() 上的點P對應的參數為
上的點P對應的參數為![]() ,Q為C
,Q為C![]() 上的動點,求
上的動點,求![]() 中點
中點![]() 到直線
到直線
![]() (t為參數)距離的最小值。
(t為參數)距離的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線![]() 的方程為
的方程為![]() ,以極點為原點,極軸所在直線為
,以極點為原點,極軸所在直線為![]() 軸建立直角坐標,直線
軸建立直角坐標,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),
為參數),![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設點![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比數列,求
成等比數列,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產的產品中分正品與次品,正品重100克,次品重110 克.現有5袋產品(每袋裝有10個產品),已知其中有且只有一袋次品(10個產品均為次品),如果將5袋產品以1-5編號,第![]() 袋取出
袋取出![]() 個產品(
個產品(![]() =1,2,3,4,5),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量
=1,2,3,4,5),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量![]() ,若次品所在的袋子的編號是2,此時的重量
,若次品所在的袋子的編號是2,此時的重量![]() =__________克;若次品所在袋子的編號是
=__________克;若次品所在袋子的編號是![]() ,此時的重量
,此時的重量![]() =_________克.
=_________克.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com