
【題目】函數f(x)的定義域為D={x|x≠0},且對于任意x1 , x2∈D,有f(x1x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判斷函數f(x)的奇偶性并證明;
(3)如果f(4)=3,f(x﹣2)+f(x+1)≤3,且f(x)在(0,+∞)上是增函數,求實數x的取值范圍.
【答案】
(1)解:對于任意x1,x2∈D,有f(x1x2)=f(x1)+f(x2),
令x1=x2=1,f(1)=f(1)+f(1)=2f(1),
∴f(1)=0,
(2)解:∵f[(﹣1)×(﹣1)]=f(﹣1)+f(﹣1)=2f(﹣1)=0,
∴f(﹣1)=0,
則f(﹣1×x)=f(﹣x)=f(﹣1)+f(x)=f(x)
∴f(x)為偶函數
(3)解:∵f(x1x2)=f(x1)+f(x2)且f(4)=3,
∴f(x﹣2)+f(x+1)≤3,即f[(x﹣2)(x+1)]≤f(4),
又∵f(x)在(0,+∞)上是增函數且f(x)為偶函數,
∴ ![]() 或
或 ![]()
解得:﹣2≤x<﹣1或﹣1<x<2或2<x≤3,
∴x的取值范圍為[﹣2,﹣1)∪(﹣1,2)∪(2,3]
【解析】(1)對于任意x1 , x2∈D,有f(x1x2)=f(x1)+f(x2),令x1=x2=1,可求f(1);(2)由(1)賦值可求f(﹣1)=0,進而可求f(﹣1×x)=f(﹣x)=f(1)+f(x)=f(x),可得f(x)為偶函數;(3)由f(4)=3,再由奇偶性和單調性,即可得到不等式組解得即可.
【考點精析】解答此題的關鍵在于理解函數單調性的判斷方法的相關知識,掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較,以及對函數的奇偶性的理解,了解偶函數的圖象關于y軸對稱;奇函數的圖象關于原點對稱.


科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程選講]在平面直角坐標系xOy中,以原點O為極點,x軸的非負半軸為極軸,建立極坐標系,曲線C1的參數方程為 ![]() 為參數),曲線C2的極坐標方程為
為參數),曲線C2的極坐標方程為 ![]() .
.
(1)求曲線C1的普通方程和曲線C2的直角坐標方程;
(2)設P為曲線C1上一點,Q曲線C2上一點,求|PQ|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的左、右焦點分別為F1 , F2 , 上頂點為B,若△BF1F2的周長為6,且點F1到直線BF2的距離為b. (Ⅰ)求橢圓C的方程;
的左、右焦點分別為F1 , F2 , 上頂點為B,若△BF1F2的周長為6,且點F1到直線BF2的距離為b. (Ⅰ)求橢圓C的方程;
(Ⅱ)設A1 , A2是橢圓C長軸的兩個端點,點P是橢圓C上不同于A1 , A2的任意一點,直線A1P交直線x=m于點M,若以MP為直徑的圓過點A2 , 求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空間幾何體ABCDEF如圖所示.已知面ABCD⊥面ADEF,ABCD為梯形,ADEF為正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G為CE的中點. (Ⅰ)求證:BG∥面ADEF;
(Ⅱ)求證:面DBG⊥面BDF.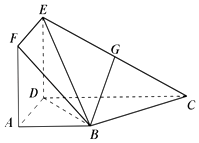
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】李冶(1192﹣1279),真定欒城(今屬河北石家莊市)人,金元時期的數學家、詩人、晚年在封龍山隱居講學,數學著作多部,其中《益古演段》主要研究平面圖形問題:求圓的直徑,正方形的邊長等,其中一問:現有正方形方田一塊,內部有一個圓形水池,其中水池的邊緣與方田四邊之間的面積為13.75畝,若方田的四邊到水池的最近距離均為二十步,則圓池直徑和方田的邊長分別是(注:240平方步為1畝,圓周率按3近似計算)( )
A.10步、50步
B.20步、60步
C.30步、70步
D.40步、80步
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*)
(Ⅰ)求m的值;
(Ⅱ)若數列{bn}滿足 ![]() =log2bn(n∈N+),求數列{(an+6)bn}的前n項和.
=log2bn(n∈N+),求數列{(an+6)bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的偶函數f(x)在[0,+∞)上遞減,若不等式f(x3﹣x2+a)+f(﹣x3+x2﹣a)≥2f(1)對x∈[0,1]恒成立,則實數a的取值范圍為( )
A.[ ![]() ,1]
,1]
B.[﹣ ![]() ,1]
,1]
C.[1,3]
D.(﹣∞,1]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點為極點,x軸的非負半軸為極軸,并在兩坐標系中取相同的長度單位,若直線l的極坐標方程是ρsin(θ+ ![]() )=2
)=2 ![]() ,且點P是曲線C:
,且點P是曲線C: ![]() (θ為參數)上的一個動點.
(θ為參數)上的一個動點.
(Ⅰ)將直線l的方程化為直角坐標方程;
(Ⅱ)求點P到直線l的距離的最大值與最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com