
【題目】已知函數![]() ,
,![]() .
.
(1)若函數![]() 有且只有一個極值點,求實數
有且只有一個極值點,求實數![]() 的取值范圍;
的取值范圍;
(2)對于函數![]() ,
,![]() ,
,![]() ,若對于區間
,若對于區間![]() 上的任意一個
上的任意一個![]() ,都有
,都有![]() ,則稱函數
,則稱函數![]() 是函數
是函數![]() ,
,![]() 在區間
在區間![]() 上的一個“分界函數”.已知
上的一個“分界函數”.已知![]() ,
,![]() ,問是否存在實數
,問是否存在實數![]() ,使得函數
,使得函數![]() 是函數
是函數![]() ,
,![]() 在區間
在區間![]() 上的一個“分界函數”?若存在,求實數
上的一個“分界函數”?若存在,求實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
試題分析:(Ⅰ)先求函數導數:![]() ,再根據函數
,再根據函數![]() 有且只有一個極值點,得
有且只有一個極值點,得![]() 在區間
在區間![]() 上有且只有一個零點,最后結合二次函數實根分布得
上有且只有一個零點,最后結合二次函數實根分布得![]() ,解得實數
,解得實數![]() 的取值范圍是
的取值范圍是![]() ;(Ⅱ)由題意得當
;(Ⅱ)由題意得當![]() 時,
時,![]() 恒成立,
恒成立,
且![]() 恒成立,即問題為恒成立問題,解決方法為轉化為對應函數最值問題:記
恒成立,即問題為恒成立問題,解決方法為轉化為對應函數最值問題:記![]() ,利用導數研究其單調變化規律,確定其最大值:當
,利用導數研究其單調變化規律,確定其最大值:當![]() 時,
時, ![]() 單調遞減,
單調遞減,![]() 最大值為
最大值為![]() ,由
,由![]() ,解得
,解得![]() ;當
;當![]() 時,
時,![]() 最大值為正無窮大,即
最大值為正無窮大,即![]() 在區間
在區間![]() 上不恒成立,同理記
上不恒成立,同理記![]() ,利用導數研究其單調變化規律,確定其最小值:由于
,利用導數研究其單調變化規律,確定其最小值:由于![]() ,所以
,所以![]() 在區間
在區間![]() 上單調遞增,其最小值為
上單調遞增,其最小值為![]() ,得
,得![]() .
.
試題解析:(1)![]() ,
,
記![]() ,
,
依題意,![]() 在區間
在區間![]() 上有且只有一個零點,
上有且只有一個零點,
∴![]() ,得實數
,得實數![]() 的取值范圍是
的取值范圍是![]() ;………………………………5分
;………………………………5分
(Ⅱ)若函數![]() 是函數
是函數![]() ,
,![]() 在區間
在區間![]() 上的一個“分界函數”,
上的一個“分界函數”,
則當![]() 時,
時,![]() 恒成立,
恒成立,
且![]() 恒成立,…………………………………………6分
恒成立,…………………………………………6分
記![]() ,
,
則![]() ,
,
若![]() ,即
,即![]() :
:
當![]() 時,
時,![]() ,
,![]() 單調遞減,且
單調遞減,且![]() ,
,
∴![]() ,解得
,解得![]() ;…………………………………………8分
;…………………………………………8分
若![]() ,即
,即![]() :
:
![]() 的圖象是開口向上的拋物線,
的圖象是開口向上的拋物線,
存在![]() ,使得
,使得![]() ,
,
從而![]() ,
,![]() 在區間
在區間![]() 上不會恒成立,…………………10分
上不會恒成立,…………………10分
記![]() ,
,
則![]() ,
,
∴![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
由![]() 恒成立,得
恒成立,得![]() ,得
,得![]() .
.
綜上,當![]() 時,函數
時,函數![]() 是函數
是函數![]() ,
,![]() 在區間
在區間![]() 上的一個“分界函數”. 13分
上的一個“分界函數”. 13分


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的兩個焦點為
)的兩個焦點為![]() ,
, ![]() ,離心率為
,離心率為![]() ,點
,點![]() ,
, ![]() 在橢圓上,
在橢圓上, ![]() 在線段
在線段![]() 上,且
上,且![]() 的周長等于
的周長等于![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過圓![]() :
: ![]() 上任意一點
上任意一點![]() 作橢圓
作橢圓![]() 的兩條切線
的兩條切線![]() 和
和![]() 與圓
與圓![]() 交于點
交于點![]() ,
, ![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分為14分)已知定義域為R的函數![]() 是奇函數.
是奇函數.
(1)求a,b的值;
(2)若對任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某冷飲店只出售一種飲品,該飲品每一杯的成本價為3元,售價為8元,每天售出的第20杯及之后的飲品半價出售.該店統計了近10天的飲品銷量,如圖所示:設![]() 為每天飲品的銷量,
為每天飲品的銷量,![]() 為該店每天的利潤.
為該店每天的利潤.

(1)求![]() 關于
關于![]() 的表達式;
的表達式;
(2)從日利潤不少于96元的幾天里任選2天,求選出的這2天日利潤都是97元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]()
![]() 的離心率為
的離心率為![]() ,
,![]() 是橢圓的右焦點,直線
是橢圓的右焦點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(I)求![]() 的方程;
的方程;
(II)設過點![]() 的動直線
的動直線![]() 與
與![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求
的面積最大時,求![]() 的方程
的方程
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示, ![]() 是某海灣旅游區的一角,為營造更加優美的旅游環境,旅游區管委會決定建立面積為
是某海灣旅游區的一角,為營造更加優美的旅游環境,旅游區管委會決定建立面積為![]() 平分千米的三角形主題游戲樂園
平分千米的三角形主題游戲樂園![]() ,并在區域
,并在區域![]() 建立水上餐廳.
建立水上餐廳.
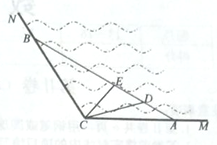
已知![]() ,
, ![]() .
.
(1)設![]() ,
, ![]() ,用
,用![]() 表示
表示![]() ,并求
,并求![]() 的最小值;
的最小值;
(2)設![]() (
(![]() 為銳角),當
為銳角),當![]() 最小時,用
最小時,用![]() 表示區域
表示區域![]() 的面積
的面積![]() ,并求
,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為實數).
為實數).
(1)當![]() 時,求函數
時,求函數![]() 的圖象在點
的圖象在點![]() 處的切線方程;
處的切線方程;
(2)設函數![]() (其中
(其中![]() 為常數),若函數
為常數),若函數![]() 在區間
在區間![]() 上不存在極值,且存在
上不存在極值,且存在![]() 滿
滿
足![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)已知![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 與圓
與圓![]() :
:![]() ,圓
,圓![]()
![]() 都相內切,即圓心
都相內切,即圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ;設
;設![]() 為曲線
為曲線![]() 上的一個不在
上的一個不在![]() 軸上的動點,
軸上的動點,![]() 為坐標原點,過點
為坐標原點,過點![]() 作
作![]() 的平行線交曲線
的平行線交曲線![]() 于
于![]() ,
,![]() 兩個不同的點.
兩個不同的點.
(1)求曲線![]() 的方程;
的方程;
(2)試探究![]() 和
和![]() 的比值能否為一個常數?若能,求出這個常數;若不能,請說明理由.
的比值能否為一個常數?若能,求出這個常數;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com