
【題目】已知向量 ![]() ,
, ![]() 滿足|
滿足| ![]() |=3,|
|=3,| ![]() |=2|
|=2| ![]() |,若|
|,若| ![]() +λ
+λ ![]() |≥3恒成立,則實數(shù)λ的取值范圍為 .
|≥3恒成立,則實數(shù)λ的取值范圍為 .
【答案】(﹣∞,﹣ ![]() )∪[
)∪[ ![]() ,+∞)
,+∞)
【解析】解:設(shè) ![]() ,
, ![]() =
= ![]() ,則
,則 ![]() =
= ![]() ,
,
設(shè)| ![]() |=x,則|OA|=x,|AB|=
|=x,則|OA|=x,|AB|= ![]() ,
,
∴ 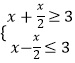 ,解得2≤x≤6.
,解得2≤x≤6.
即2≤| ![]() |≤6.
|≤6.
∵| ![]() |=2|
|=2| ![]() |,
|,
∴ ![]() =4(9﹣2
=4(9﹣2 ![]() +
+ ![]() 2),即3
2),即3 ![]() ﹣8
﹣8 ![]() +36=0,
+36=0,
∴ ![]() =
= ![]() +
+ ![]() ,
,
∵| ![]() +λ
+λ ![]() |≥3恒成立,
|≥3恒成立,
∴ ![]() +2λ(
+2λ( ![]() +
+ ![]() )+9λ2≥9,
)+9λ2≥9,
令f( ![]() 2)=(1+
2)=(1+ ![]() λ)
λ) ![]() 2+9λ+9λ2﹣9,則fmin(
2+9λ+9λ2﹣9,則fmin( ![]() )≥0,
)≥0, ![]() ∈[4,36].
∈[4,36].
(i)若1+ ![]() λ=0即λ=﹣
λ=0即λ=﹣ ![]() 時,f(
時,f( ![]() )=9λ+9λ2﹣9=﹣5,不符合題意;
)=9λ+9λ2﹣9=﹣5,不符合題意;
(ii)若1+ ![]() >0即λ>﹣
>0即λ>﹣ ![]() 時,f(
時,f( ![]() )為增函數(shù),故fmin(
)為增函數(shù),故fmin( ![]() )=f(4)=9λ2+12λ﹣5≥0,
)=f(4)=9λ2+12λ﹣5≥0,
解得λ ![]() 或λ≤﹣
或λ≤﹣ ![]() ,∴λ≥
,∴λ≥ ![]() .
.
(iii)若1+ ![]() <0即λ<﹣
<0即λ<﹣ ![]() 時,f(
時,f( ![]() )為減函數(shù),故fmin(
)為減函數(shù),故fmin( ![]() )=f(36)=9λ2+36λ+27≥0,
)=f(36)=9λ2+36λ+27≥0,
解得λ≤1或λ≥3.∴λ<﹣ ![]() .
.
綜上,λ<﹣ ![]() 或λ
或λ ![]() .
.
所以答案是:(﹣∞,﹣ ![]() )∪[
)∪[ ![]() ,+∞).
,+∞).


 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在棱臺ABC﹣FED中,△DEF與△ABC分別是棱長為1與2的正三角形,平面ABC⊥平面BCDE,四邊形BCDE為直角梯形,BC⊥CD,CD=1,N為CE中點, ![]() .
.
(1)λ為何值時,MN∥平面ABC?
(2)在(1)的條件下,求直線AN與平面BMN所成角的正弦值. 
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩袋中各裝有大小相同的小球9個,其中甲袋中紅色、黑色、白色小球的個數(shù)分別為2、3、4,乙袋中紅色、黑色、白色小球的個數(shù)均為3,某人用左手從甲袋中取球,用右手從乙袋中取球,
(1)若左右手各取一球,求兩只手中所取的球顏色不同的概率;
(2)若一次在同一袋中取出兩球,如果兩球顏色相同則稱這次取球獲得成功.某人第一次左手先取兩球,第二次右手再取兩球,記兩次取球的獲得成功的次數(shù)為隨機變量X,求X的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某汽車的使用年數(shù)x與所支出的維修費用y的統(tǒng)計數(shù)據(jù)如表:
使用年數(shù)x(單位:年) | 1 | 2 | 3 | 4 | 5 |
維修總費用y(單位:萬元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根據(jù)上表可得y關(guān)于x的線性回歸方程 ![]() =
= ![]() x﹣0.69,若該汽車維修總費用超過10萬元就不再維修,直接報廢,據(jù)此模型預(yù)測該汽車最多可使用( )
x﹣0.69,若該汽車維修總費用超過10萬元就不再維修,直接報廢,據(jù)此模型預(yù)測該汽車最多可使用( )
A.8年
B.9年
C.10年
D.11年
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中.圓C的參數(shù)方程為 ![]() (α為參數(shù)),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,點D的極坐標為(ρ1 , π).
(α為參數(shù)),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,點D的極坐標為(ρ1 , π).
(1)求圓C的極坐標方程;
(2)過點D作圓C的切線,切點分別為A,B,且∠ADB=60°,求ρ1 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓方程為 ![]() +y2=1,圓C:(x﹣1)2+y2=r2 .
+y2=1,圓C:(x﹣1)2+y2=r2 . 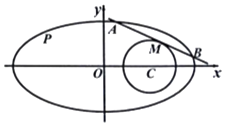
(Ⅰ)求橢圓上動點P與圓心C距離的最小值;
(Ⅱ)如圖,直線l與橢圓相交于A、B兩點,且與圓C相切于點M,若滿足M為線段AB中點的直線l有4條,求半徑r的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1所有的棱長均為2,A1B= ![]() ,A1B⊥AC.
,A1B⊥AC. 
(Ⅰ)求證:A1C1⊥B1C;
(Ⅱ)求直線AC和平面ABB1A1所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=  ,若f(x)的兩個零點分別為x1 , x2 , 則|x1﹣x2|=( )
,若f(x)的兩個零點分別為x1 , x2 , 則|x1﹣x2|=( )
A.![]()
B.1+ ![]()
C.2
D.![]() +ln2
+ln2
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}中,a2=2,其前n項和Sn滿足: ![]() (n∈N*).
(n∈N*).
(Ⅰ)求數(shù)列{an}的通項公式;
(Ⅱ)若 ![]() ,求數(shù)列{bn}的前n項和Tn .
,求數(shù)列{bn}的前n項和Tn .
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com