
【題目】為了研究“教學方式”對教學質量的影響,某高中老師分別用兩種不同的教學方式對入學數學平均分數和優秀率都相同的甲、乙兩個高一新班進行教學(勤奮程度和自覺性都一樣).以下莖葉圖為甲、乙兩班(每班均為20人)學生的數學期末考試成績.

(1)現從甲班數學成績不低于80分的同學中隨機抽取兩名同學,求成績為87分的同學至少有一名被抽中的概率;
(2)學校規定:成績不低于75分的為優秀,請填寫下面的![]() 列聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
列聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
甲班 | 乙班 | 合計 | |
優秀 | |||
不優秀 | |||
合計 |
下面臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| span>2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() )
)
【答案】(1)![]() ;(2)列聯表見解析,有
;(2)列聯表見解析,有![]() 的把握認為成績優秀與教學方式有關.
的把握認為成績優秀與教學方式有關.
【解析】
試題分析:(1)甲班數學成績不低于![]() 分的同學有
分的同學有![]() 個,其中分數不是
個,其中分數不是![]() 的同學不妨記為
的同學不妨記為![]() ,
,![]() ,
,![]() ,分數為
,分數為![]() 的同學不妨記為
的同學不妨記為![]() ,
,![]() ,寫出從
,寫出從![]() 位同學任選
位同學任選![]() 名所有共
名所有共![]() 個基本事件,其中事件“成績為
個基本事件,其中事件“成績為![]() 分的同學至少有一名被抽中”包含了
分的同學至少有一名被抽中”包含了![]() 個基本事件,從而求得成績為
個基本事件,從而求得成績為![]() 分的同學至少有一名被抽中的概率;(2)根據所給數據填入表格,利用公式求得
分的同學至少有一名被抽中的概率;(2)根據所給數據填入表格,利用公式求得![]() 的值,從而得出結論.
的值,從而得出結論.
試題解析:(1)甲班數學成績不低于80分的同學有5個,其中分數不是87的同學不妨記為![]() ,
,![]() ,
,![]() ,分數為
,分數為![]() 的同學不妨記為
的同學不妨記為![]() ,
,![]() ;
;
從5位同學任選2名共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 10個基本事件.
10個基本事件.
事件“成績為87分的同學至少有一名被抽中”包含了7個基本事件,
所以![]() (成績為87分的同學至少有一名被抽中)
(成績為87分的同學至少有一名被抽中)![]() .
.
(2)
甲班 | 乙班 | 合計 | |
優秀 | 6 | 14 | 20 |
不優秀 | 14 | 6 | 20 |
合計 | 20 | 20 | 40 |
![]() ,
,
∵![]() ,
,
∴在犯錯誤的概率不超過![]() 的前提下認為成績優秀與教學方式有關(我們有
的前提下認為成績優秀與教學方式有關(我們有![]() 的把握認為成績優秀教學方式有關).
的把握認為成績優秀教學方式有關).


科目:高中數學 來源: 題型:
【題目】已知拋物線y2=2px(p>0)的焦點為F,A是拋物線上橫坐標為4,且位于x軸上方的點,A到拋物線準線的距離等于5,過A作AB垂直于y軸,垂足為B,OB的中點為M.
(1)求拋物線的方程;
(2)以M為圓心,MB為半徑作圓M,當K(m,0)是x軸上一動點時,討論直線AK與圓M的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)求函數![]() 在
在![]() 上的最小值;
上的最小值;
(2)對一切![]() ,
,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)探討函數![]() 是否存在零點?若存在,求出函數
是否存在零點?若存在,求出函數![]() 的零點;若不存在,請說明理由.
的零點;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一盒中放有的黑球和白球,其中黑球4個,白球5個.
(1)從盒中同時摸出兩個球,求兩球顏色恰好相同的概率.
(2)從盒中摸出一個球,放回后再摸出一個球,求兩球顏色恰好不同的概率.
(3)從盒中不放回的每次摸一球,若取到白球則停止摸球,求取到第三次時停止摸球的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】東亞運動會將于2013年10月6日在天津舉行.為了搞好接待工作,組委會打算學習北京奧運會招募大量志愿者的經驗,在某學院招募了16名男志愿者和14名女志愿者,調查發現,男女志愿者中分別有10人和6人喜愛運動,其余人不喜歡運動.
(1)根據以上數據完成以下2×2列聯表:
喜愛運動 | 不喜愛運動 | 總計 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
總計 | 30 |
(2)根據列聯表的獨立性檢驗,能否在犯錯誤的概率不超過0.10的前提下認為性別與喜愛運動有關?
(3)如果從喜歡運動的女志愿者中(其中恰有4人會外語),抽取2名負責翻譯工作,那么抽出的志愿者中至少有1人能勝任翻譯工作的概率是多少?
參考公式:K2=![]() ,其中
,其中
n=a+b+c+d.
參考數據:
P(K2≥k) | 0.40 | 0.25 | 0.10 | 0.010 |
k | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現如今,“網購”一詞不再新鮮,越來越多的人已經接受并喜歡了這種購物方式,但隨之也出現了商品質量不能保證與信譽不好等問題,因此,相關管理部門制定了針對商品質量與服務的評價體系,現從評價系統中選出成功交易200例,并對其評價進行統計:對商品的好評率為0.6,對服務的好評率為0.75,其中對商品和服務都做出好評的交易為80次.
(1)依據題中的數據完成下表: 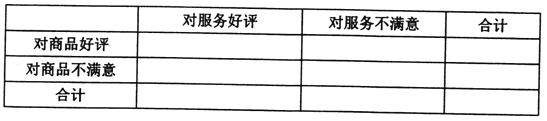
(2)通過計算說明,能否有99.9%的把握認為“商品好評與服務好評”有關;

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,六面體ABCDHEFG中,四邊形ABCD為菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
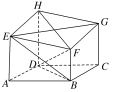
(1)求證:EG⊥DF;
(2)求BE與平面EFGH所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com