【題目】設函數
，
是函數
的導數.
（1）若
，證明在區間
上沒有零點；
（2）在
上
恒成立，求
的取值范圍.
【答案】（1）證明見解析（2）
【解析】
（1）先利用導數的四則運算法則和導數公式求出
，再由函數的導數可知，
函數在
上單調遞增，在
上單調遞減，而
，
，可知
在區間
上恒成立，即在區間上沒有零點；
（2）由題意可將
轉化為
，構造函數
，
利用導數討論研究其在
上的單調性，由
，即可求出
的取值范圍．
（1）若
，則
，
，
設
，則
，
，
，故函數
是奇函數．
當
時，
，
，這時
，
又函數是奇函數，所以當
時，
.
綜上，當時，函數單調遞增；當時，函數單調遞減.
又
，
，
故在區間上恒成立，所以在區間上沒有零點.
（2）
，由
，所以
恒成立，
若，則，設，
.
故當
時，
，又
，所以當
時，
，滿足題意；
當
時，有
，與條件矛盾，舍去；
當
時，令
，則
，
又
，故
在區間
上有無窮多個零點，
設最小的零點為
，
則當
時，
，因此
在
上單調遞增.
，所以
.
于是，當時，
，得
，與條件矛盾.
故的取值范圍是.
黃岡創優卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝﹣x3+1+a（
x≤e，e是自然對數的底）與g（x）＝3lnx的圖象上存在關于x軸對稱的點，則實數a的取值范圍是（ ）
A.[0，e3﹣4]B.[0，
2]
C.[2，e3﹣4]D.[e3﹣4，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
中，
，
，
，
是
的中點，E是棱
上一動點．
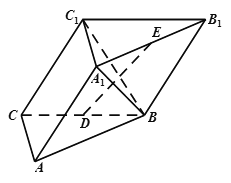
（1）若E是棱的中點，證明：
平面
；
（2）求二面角
的余弦值；
（3）是否存在點E，使得
，若存在，求出E的坐標，若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某縣為了幫助農戶脫貧致富，鼓勵農戶利用荒地山坡種植果樹，某農戶考察了三種不同的果樹苗
、
、
．經過引種實驗發現，引種樹苗的自然成活率為
，引種樹苗、的自然成活率均為
．
（1）任取樹苗、、各一棵，估計自然成活的棵數為
，求的分布列及其數學期望；
（2）將（1）中的數學期望取得最大值時
的值作為種樹苗自然成活的概率．該農戶決定引種
棵種樹苗，引種后沒有自然成活的樹苗有
的樹苗可經過人工栽培技術處理，處理后成活的概率為
，其余的樹苗不能成活．
①求一棵種樹苗最終成活的概率；
②若每棵樹苗引種最終成活可獲利
元，不成活的每棵虧損
元，該農戶為了獲利期望不低于
萬元，問至少要引種種樹苗多少棵？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量指數AQI是反映空氣質量狀況的指數，AQI指數值越小，表明空氣質量越好，其對應關系如下表：
AQI指數值 | 0～50 | 51～100 | 101～150 | 151～200 | 201～300 | ＞300 |
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
下圖是某市10月1日—20日AQI指數變化趨勢：
下列敘述錯誤的是
A. 這20天中AQI指數值的中位數略高于100
B. 這20天中的中度污染及以上的天數占
C. 該市10月的前半個月的空氣質量越來越好
D. 總體來說，該市10月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在底面是菱形的四棱錐
中, 
平面
， 
，點
分別為
的中點，設直線
與平面
交于點
.
（1）已知平面
平面
，求證： 
.
（2）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的離心率
，點
，點
、
分別為橢圓的上頂點和左焦點，且
.
（1）求橢圓的方程；
（2）若過定點
的直線
與橢圓交于
，
兩點（在
，之間）設直線的斜率
，在
軸上是否存在點
，使得以
，
為鄰邊的平行四邊形為菱形？如果存在，求出
的取值范圍？如果不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
