
已知常數(shù)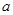 、
、 、
、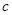 都是實(shí)數(shù),函數(shù)
都是實(shí)數(shù),函數(shù)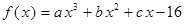 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為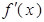 ,
,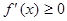 的解集為
的解集為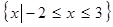 .
.
(Ⅰ)若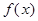 的極大值等于
的極大值等于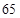 ,求
,求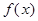 的極小值;
的極小值;
(Ⅱ)設(shè)不等式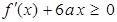 的解集為集合
的解集為集合 ,當(dāng)
,當(dāng) 時(shí),函數(shù)
時(shí),函數(shù)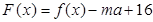 只有一個(gè)零點(diǎn),求實(shí)數(shù)
只有一個(gè)零點(diǎn),求實(shí)數(shù)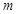 的取值范圍.
的取值范圍.
(Ⅰ)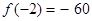 ;(Ⅱ)當(dāng)
;(Ⅱ)當(dāng)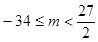 或
或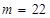 時(shí),函數(shù)
時(shí),函數(shù)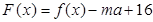 在
在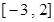 上只有一個(gè)零點(diǎn).
上只有一個(gè)零點(diǎn).
解析試題分析::1.第(Ⅰ)的解答還是要破費(fèi)周折的.首先要求出導(dǎo)函數(shù)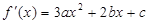 .
.
然后根據(jù)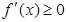 的解集為
的解集為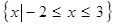 ,通過(guò)解混合組,得到
,通過(guò)解混合組,得到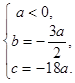 進(jìn)而得到
進(jìn)而得到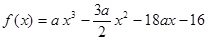 .接下來(lái)通過(guò)研究函數(shù)
.接下來(lái)通過(guò)研究函數(shù)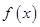 的單調(diào)性,由
的單調(diào)性,由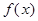 的極大值等于
的極大值等于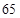 ,可解得
,可解得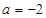 ,這樣就可以求出
,這樣就可以求出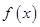 的極小值
的極小值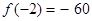 .2.第(Ⅱ)問(wèn)先由不等式
.2.第(Ⅱ)問(wèn)先由不等式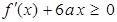 的解集為集合
的解集為集合 ,可以解得
,可以解得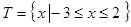 .然后研究
.然后研究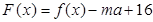 的單調(diào)性,值得注意的是
的單調(diào)性,值得注意的是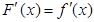 ,換句話(huà)說(shuō)方程兩邊對(duì)
,換句話(huà)說(shuō)方程兩邊對(duì)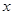 求導(dǎo)數(shù),
求導(dǎo)數(shù),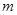 、
、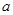 應(yīng)看作是常數(shù).單調(diào)性弄清楚后,還要比較
應(yīng)看作是常數(shù).單調(diào)性弄清楚后,還要比較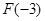 、
、 的大小.然后根據(jù)
的大小.然后根據(jù) 只有一個(gè)零點(diǎn),列出
只有一個(gè)零點(diǎn),列出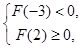 或
或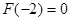 ,最后解之即可.值得注意的是,很多考生漏了
,最后解之即可.值得注意的是,很多考生漏了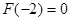 .
.
試題解析:(Ⅰ)∵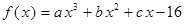 ,∴
,∴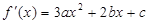 .
.
∵不等式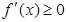 的解集為
的解集為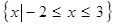 ,
,
∴不等式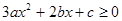 的解集為
的解集為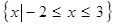 .
.
∴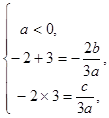 即
即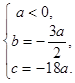
∴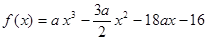 ,
,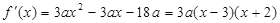 .
.
∴當(dāng)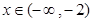 或
或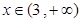 時(shí),
時(shí),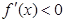 ,即
,即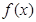 為單調(diào)遞減函數(shù);
為單調(diào)遞減函數(shù);
當(dāng)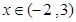 時(shí),
時(shí),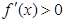 ,即
,即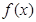 為單調(diào)遞增函數(shù).
為單調(diào)遞增函數(shù).
∴當(dāng) 時(shí),
時(shí),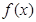 取得極大值,當(dāng)
取得極大值,當(dāng)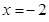 時(shí),
時(shí),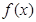 取得極小值.
取得極小值.
由已知得 ,解得
,解得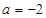 .
.
∴ .
.
∴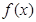 的極小值
的極小值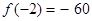 .
.
(Ⅱ)∵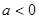 ,
,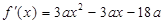 ,
,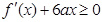 ,
,
∴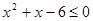 ,解得
,解得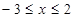 ,即
,即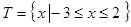 .
.
∵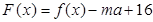 ,∴
,∴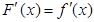 .
.
∴當(dāng)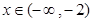 或
或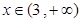 時(shí),
時(shí),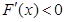 ,即
,即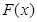 為單調(diào)遞減函數(shù);
為單調(diào)遞減函數(shù);
當(dāng)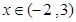 時(shí),
時(shí), ,即
,即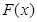 為單調(diào)遞增函數(shù).
為單調(diào)遞增函數(shù).
∴當(dāng)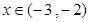 時(shí),
時(shí),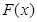 為單調(diào)遞減函數(shù);
為單調(diào)遞減函數(shù);
當(dāng)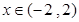 時(shí),
時(shí),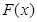 為單調(diào)遞增函數(shù).
為單調(diào)遞增函數(shù).
∵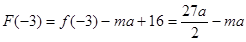 ,
,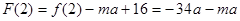 ,
,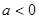 ,
,
∴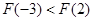 .
.
∴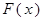 在
在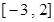 上只有一個(gè)零點(diǎn)
上只有一個(gè)零點(diǎn)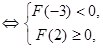



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)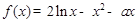 .
.
(Ⅰ)當(dāng)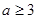 時(shí),討論函數(shù)
時(shí),討論函數(shù)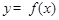 在[
在[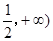 上的單調(diào)性;
上的單調(diào)性;
(Ⅱ)如果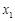 ,
,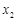
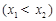 是函數(shù)
是函數(shù)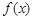 的兩個(gè)零點(diǎn),
的兩個(gè)零點(diǎn),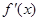 為函數(shù)
為函數(shù)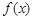 的導(dǎo)數(shù),證明:
的導(dǎo)數(shù),證明: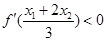 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)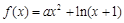 .
.
(Ⅰ)當(dāng)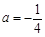 時(shí),求函數(shù)
時(shí),求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)當(dāng)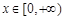 時(shí),不等式
時(shí),不等式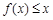 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)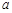 的取值范圍.
的取值范圍.
(Ⅲ)求證: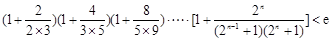 (
(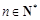 ,e是自然對(duì)數(shù)的底數(shù)).
,e是自然對(duì)數(shù)的底數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)f(x)= -
-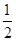 alnx,a∈R.
alnx,a∈R.
(Ⅰ)當(dāng)f(x)存在最小值時(shí),求其最小值φ(a)的解析式;
(Ⅱ)對(duì)(Ⅰ)中的φ(a),
(ⅰ)當(dāng)a∈(0,+∞)時(shí),證明:φ(a)≤1;
(ⅱ)當(dāng)a>0,b>0時(shí),證明:φ′( )≤
)≤ ≤φ′(
≤φ′( ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù) (
(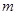 ,
,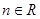 ,
,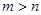 且
且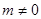 )的圖象在
)的圖象在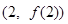 處的切線(xiàn)與
處的切線(xiàn)與 軸平行.
軸平行.
(1)確定實(shí)數(shù)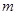 、
、 的正、負(fù)號(hào);
的正、負(fù)號(hào);
(2)若函數(shù)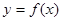 在區(qū)間
在區(qū)間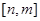 上有最大值為
上有最大值為 ,求
,求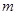 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù) ,
, ,且函數(shù)
,且函數(shù) 在點(diǎn)
在點(diǎn) 處的切線(xiàn)方程為
處的切線(xiàn)方程為 .
.
(Ⅰ)求函數(shù) 的解析式;
的解析式;
(Ⅱ)設(shè)點(diǎn) ,當(dāng)
,當(dāng) 時(shí),直線(xiàn)
時(shí),直線(xiàn) 的斜率恒小于
的斜率恒小于 ,試求實(shí)數(shù)
,試求實(shí)數(shù) 的取值范圍;
的取值范圍;
(Ⅲ)證明: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知 在
在 處取得極值。
處取得極值。
(Ⅰ)證明: ;
;
(Ⅱ)是否存在實(shí)數(shù) ,使得對(duì)任意
,使得對(duì)任意 ?若存在,求
?若存在,求 的所有值;若不存在,說(shuō)明理由。
的所有值;若不存在,說(shuō)明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)函數(shù) (
( 為常數(shù))
為常數(shù))
(Ⅰ) =2時(shí),求
=2時(shí),求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)當(dāng) 時(shí),
時(shí), ,求
,求 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)l為曲線(xiàn)C: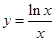 在點(diǎn)(1,0)處的切線(xiàn).
在點(diǎn)(1,0)處的切線(xiàn).
(I)求l的方程;
(II)證明:除切點(diǎn)(1,0)之外,曲線(xiàn)C在直線(xiàn)l的下方
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com