Question

若函數f（x）=ax³+bx²+cx+d的圖象如圖所示，則一定有（　　）

• A、b＞0，c＞0
• B、b＜0，c＞0
• C、b＞0，c＜0
• D、b＜0，c＜0

Answer 1

考點：函數的圖象

專題：函數的性質及應用

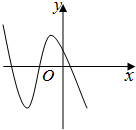
分析：由已知中函數f（x）=ax³+bx²+cx+d的圖象，根據其與y軸交點的位置，可以判斷d的符號，進而根據其單調性和極值點的位置，可以判斷出其中導函數圖象的開口方向（可判斷a的符號）及對應函數兩個根的情況，結合韋達定理，可分析出b，c的符號，進而得到答案．

解答： 解：∵函數f（x）=ax³+bx²+cx+d的圖象與y軸交點的縱坐標為正，故d＞0；
∵f（x）=ax³+bx²+cx+d的圖象有兩個遞減區間，有一個遞增區間，
∴f′（x）=3ax²+2bx+c的圖象開口方向朝下，且于x軸有兩個交點，故a＜0，
又∵f（x）=ax³+bx²+cx+d的圖象的極小值點和極大值點在y軸左側，且極大值點離y軸近，
∴f′（x）=3ax²+2bx+c=0的兩根x₁，x₂滿足，
x₁+x₂＜0，則b＜0，x₁•x₂＞0，則c＜0，
綜上a＜0，b＜0，c＜0，d＞0，
故選：D．

點評：本題考查的知識點是函數的圖象與圖象變化，其中根據圖象的形狀分析其導函數的性質是解答本題的關鍵，同時由于本題涉及到導數，二次函數的圖象和性質，函數的單調性，函數取極值的條件等諸多難點，屬于中檔題