
【題目】等差數列{an}中,已知an>0,a1+a2+a3=15,且a1+2,a2+5,a3+13構成等比數列{bn}的前三項.
(1)求數列{an},{bn}的通項公式;
(2)求數列{anbn}的前n項和Tn .
【答案】
(1)解:設設等差數列的公差為d,則由已知得:a1+a2+a3=3a2=15,即a2=5,
又(5﹣d+2)(5+d+13)=100,解得d=2或d=﹣13(舍),
a1=a2﹣d=3,
∴an=a1+(n﹣1)×d=2n+1,
又b1=a1+2=5,b2=a2+5=10,
∴q=2
∴ ![]()
(2)解:∵ ![]() ,
,
![]() ,
,
兩式相減得 ![]() ,
,
則 ![]()
【解析】(1)利用等差數列的通項公式及其性質可得an . 再利用等比數列的通項公式即可得出bn . (2)利用“錯位相減法”與等比數列的前n項和公式即可得出.
【考點精析】解答此題的關鍵在于理解數列的前n項和的相關知識,掌握數列{an}的前n項和sn與通項an的關系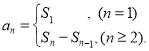 ,以及對數列的通項公式的理解,了解如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
,以及對數列的通項公式的理解,了解如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,M,N,P分別是B1B,B1C1 , CD的中點,則MN與D1P所成角的余弦值為( ) 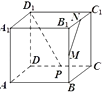
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某污水處理廠要在一個矩形污水處理池(ABCD)的池底水平鋪設污水凈化管道(Rt△FHE,H是直角頂點)來處理污水,管道越長,污水凈化效果越好.設計要求管道的接口H是AB的中點,E,F分別落在線段BC,AD上.已知AB=20米, ![]() 米,記∠BHE=θ.
米,記∠BHE=θ. 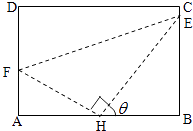
(1)試將污水凈化管道的長度L表示為θ的函數,并寫出定義域;
(2)若 ![]() ,求此時管道的長度L;
,求此時管道的長度L;
(3)當θ取何值時,污水凈化效果最好?并求出此時管道的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 的極坐標方程化為直坐標方程,并說明曲線
的極坐標方程化為直坐標方程,并說明曲線![]() 的形狀;
的形狀;
(2)若直線![]() 經過點
經過點![]() ,求直線
,求直線![]() 被曲線
被曲線![]() 截得的線段
截得的線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}滿足 ![]() =1,公差d∈(﹣1,0),當且僅當n=9時,數列{an}的前n項和Sn取得最大值,求該數列首項a1的取值范圍( )
=1,公差d∈(﹣1,0),當且僅當n=9時,數列{an}的前n項和Sn取得最大值,求該數列首項a1的取值范圍( )
A.( ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com