
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且PC=BC=2AD=2CD=2
,且PC=BC=2AD=2CD=2![]() ,
,![]() .
.
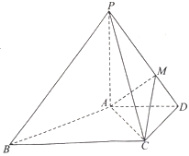
(1)![]() 平面
平面![]() ;
;
(2)已知點![]() 在線段
在線段![]() 上,且
上,且![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見證明;(2)![]()
【解析】
(1)要證![]() 平面
平面![]() ,只需證明
,只需證明![]() ,
,![]() 即可.由勾股定理易證
即可.由勾股定理易證![]() ,又由
,又由![]() 可得
可得 ![]() 平面
平面![]() ,進而可得
,進而可得![]() ,因此可得結論成立.
,因此可得結論成立.
(2)法一:可由等體積法求解,由![]() ,易得點
,易得點![]() 到平面
到平面![]() 的距離;
的距離;
法二:先證![]() ,由三角形相似,也可求出點
,由三角形相似,也可求出點![]() 到平面
到平面![]() 的距離.
的距離.
(1)∵在底面![]() 中,
中,![]() ,
,![]()
且![]()
∴![]() ,
,![]() ∴
∴![]()
又∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() 又∵
又∵![]() 平面
平面![]() ∴
∴![]()
∵![]() ,
,![]() ∴
∴![]()
又∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]()
(2)方法一:在線段![]() 上取點
上取點![]() ,使
,使![]() ,則
,則![]()
又由(1)得![]() 平面
平面![]() ,
,![]() 平面
平面![]()
又∵![]() 平面
平面![]() ,∴
,∴![]()
作![]() 于
于![]() 又∵
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() 又∵
又∵![]() 平面
平面![]() ∴
∴![]()
設點![]() 到平面
到平面![]() 的距離為
的距離為![]()
則由![]() 得
得![]()
∴點![]() 到平面
到平面![]() 的距離
的距離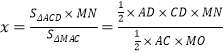
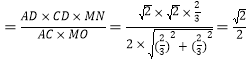
方法二:由(1)知![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∵![]() ,平面
,平面![]() 平面
平面![]() ∴
∴![]() 平面
平面![]()
∴平面![]() 平面
平面![]() ①
①
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ∴
∴![]()
![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ∴
∴![]() ∴
∴![]() ②
②
平面![]() 平面
平面![]() ③
③
由①②③得![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
又∵平面![]() 平面
平面![]() ∴過
∴過![]() 作
作![]() 交
交![]() 于點
于點![]() ∴
∴![]() 平面
平面![]()
即![]() 的長就是點
的長就是點![]() 到平面
到平面![]() 的距離.
的距離.
在![]() 中,
中,![]() ,
,![]()
∴![]()


科目:高中數學 來源: 題型:
【題目】[2019·清遠期末]一只紅鈴蟲的產卵數![]() 和溫度
和溫度![]() 有關,現收集了4組觀測數據列于下表中,根據數據作出散點圖如下:
有關,現收集了4組觀測數據列于下表中,根據數據作出散點圖如下:
溫度 | 20 | 25 | 30 | 35 |
產卵數 | 5 | 20 | 100 | 325 |

(1)根據散點圖判斷![]() 與
與![]() 哪一個更適宜作為產卵數
哪一個更適宜作為產卵數![]() 關于溫度
關于溫度![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程(數字保留2位小數);
的回歸方程(數字保留2位小數);
(3)要使得產卵數不超過50,則溫度控制在多少![]() 以下?(最后結果保留到整數)
以下?(最后結果保留到整數)
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C:![]()
(1)若圓C與x軸相切,求實數a的值;
(2)若M,N為圓C上不同的兩點,過點M,N分別作圓C的切線![]() ,若
,若![]() 與
與![]() 相交于點P,圓C上異于M,N另有一點Q,滿足
相交于點P,圓C上異于M,N另有一點Q,滿足![]() ,若直線
,若直線![]() :
:![]() 上存在唯一的一個點T,使得
上存在唯一的一個點T,使得![]() ,求實數a的值.
,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
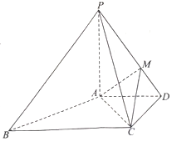
(1)證明:![]() 平面
平面![]() ;
;
(2)在線段![]() 上,是否存在一點
上,是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ) ![]() 的部分圖象如圖所示.
的部分圖象如圖所示.

(1)求函數y=f(x)的解析式;
(2)求f(x)的單調減區間
(3)當![]() 時,求f(x)的取值范圍.
時,求f(x)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲地到乙地要經過3個十字路口,設各路口信號燈工作相互獨立,且在各路口遇到紅燈的概率分別為![]() .
.
(Ⅰ)設![]() 表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量
表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)若有2輛車獨立地從甲地到乙地,求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 和橢圓
和橢圓![]() . 直線
. 直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() .
.
(Ⅰ) 求橢圓![]() 的離心率;
的離心率;
(Ⅱ) 當![]() 時,求
時,求![]() 的面積;
的面積;
(Ⅲ)設直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,當
,當![]() 為
為![]() 中點時,求
中點時,求![]() 的值 .
的值 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com