
【題目】函數(shù)f(x)=Asin(ωx+φ) ![]() 的部分圖象如圖所示.
的部分圖象如圖所示.

(1)求函數(shù)y=f(x)的解析式;
(2)求f(x)的單調(diào)減區(qū)間
(3)當(dāng)![]() 時,求f(x)的取值范圍.
時,求f(x)的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() .
.
【解析】
(1)圖象離平衡位置最高值為1,可知A=1,又從圖可看出周期的四分之一為![]() ,根據(jù)
,根據(jù)![]() 可求得
可求得![]() 的值,對于
的值,對于![]() 可通過代入(
可通過代入(![]() ,1)點(diǎn)求得,但要注意
,1)點(diǎn)求得,但要注意![]() 的范圍;(2)由(1)可得解析式為
的范圍;(2)由(1)可得解析式為![]() ,利用正弦型函數(shù)單調(diào)性即可求得結(jié)果;(3)本小題考查三角函數(shù)求值域問題,由
,利用正弦型函數(shù)單調(diào)性即可求得結(jié)果;(3)本小題考查三角函數(shù)求值域問題,由![]() 的范圍可先求出
的范圍可先求出![]() 的范圍,結(jié)合正弦函數(shù)圖象可求出sin(x+
的范圍,結(jié)合正弦函數(shù)圖象可求出sin(x+![]() )的取值范圍.
)的取值范圍.
(1)由圖象得A=1,![]() ,所以
,所以![]() ,則
,則![]() .
.
將點(diǎn)(![]() ,1)代入得sin(
,1)代入得sin(![]() +
+![]() )=1,而-
)=1,而-![]() <
<![]() <
<![]() ,所以
,所以![]() =
=![]() ,
,
因此函數(shù)f(x)=sin(x+![]() ).
).
(2)![]()
![]() ,當(dāng)
,當(dāng)![]() ,
,![]() 時,單調(diào)遞減,
時,單調(diào)遞減,
![]() f(x)的單調(diào)減區(qū)間為
f(x)的單調(diào)減區(qū)間為![]() ,
,![]()
(3)由于![]() ,-
,-![]() ≤x+
≤x+![]() ≤
≤![]() ,所以-1≤sin(x+
,所以-1≤sin(x+![]() )≤
)≤![]() ,
,
所以![]() 的取值范圍[-1,
的取值范圍[-1,![]() ].
].



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠生產(chǎn)某種產(chǎn)品的年固定成本為250萬元,每生產(chǎn)x千件,需另投入成本為C(x),當(dāng)年產(chǎn)量不足80千件時,C(x)=![]() x2+10x(萬元).當(dāng)年產(chǎn)量不小于80千件時,C(x)=51x+
x2+10x(萬元).當(dāng)年產(chǎn)量不小于80千件時,C(x)=51x+![]() -1 450(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產(chǎn)的商品能全部售完.
-1 450(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產(chǎn)的商品能全部售完.
(1)寫出年利潤L(x)(萬元)關(guān)于年產(chǎn)量x(千件)的函數(shù)解析式;
(2)當(dāng)年產(chǎn)量為多少千件時,該廠在這一商品的生產(chǎn)中所獲利潤最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】平面直角坐標(biāo)系中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,(
,(![]() 為參數(shù)).以原點(diǎn)為極點(diǎn),
為參數(shù)).以原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出直線![]() 的極坐標(biāo)方程與曲線
的極坐標(biāo)方程與曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知與直線![]() 平行的直線
平行的直線![]() 過點(diǎn)
過點(diǎn)![]() ,且與曲線
,且與曲線![]() 交于
交于![]() 兩點(diǎn),試求
兩點(diǎn),試求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且PC=BC=2AD=2CD=2
,且PC=BC=2AD=2CD=2![]() ,
,![]() .
.
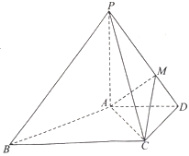
(1)![]() 平面
平面![]() ;
;
(2)已知點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某運(yùn)動員每次投籃命中的概率等于![]() .現(xiàn)采用隨機(jī)模擬的方法估計該運(yùn)動員三次投籃恰有兩次命中的概率:先由計算器產(chǎn)生0到9之間取整數(shù)值的隨機(jī)數(shù),指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三個隨機(jī)數(shù)為一組,代表三次投籃的結(jié)果.經(jīng)隨機(jī)模擬產(chǎn)生了如下20組隨機(jī)數(shù):
.現(xiàn)采用隨機(jī)模擬的方法估計該運(yùn)動員三次投籃恰有兩次命中的概率:先由計算器產(chǎn)生0到9之間取整數(shù)值的隨機(jī)數(shù),指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三個隨機(jī)數(shù)為一組,代表三次投籃的結(jié)果.經(jīng)隨機(jī)模擬產(chǎn)生了如下20組隨機(jī)數(shù):
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據(jù)此估計,該運(yùn)動員三次投籃恰有兩次命中的概率為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】P是圓![]() 上的動點(diǎn),P點(diǎn)在x軸上的射影是D,點(diǎn)M滿足
上的動點(diǎn),P點(diǎn)在x軸上的射影是D,點(diǎn)M滿足![]() .
.
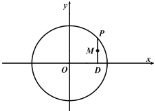
(1)求動點(diǎn)M的軌跡C的方程,并說明軌跡是什么圖形;
(2)過點(diǎn)![]() 的直線l與動點(diǎn)M的軌跡C交于不同的兩點(diǎn)A,B,求以OA,OB為鄰邊的平行四邊形OAEB的頂點(diǎn)E的軌跡方程.
的直線l與動點(diǎn)M的軌跡C交于不同的兩點(diǎn)A,B,求以OA,OB為鄰邊的平行四邊形OAEB的頂點(diǎn)E的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(Ⅰ)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(Ⅱ)求證: 當(dāng)![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線C的參數(shù)方程為![]() (t為參數(shù)),以原點(diǎn)O為極點(diǎn),x軸的非負(fù)半軸為極軸建立極坐標(biāo)系,過極點(diǎn)的兩射線
(t為參數(shù)),以原點(diǎn)O為極點(diǎn),x軸的非負(fù)半軸為極軸建立極坐標(biāo)系,過極點(diǎn)的兩射線![]() 、
、![]() 相互垂直,與曲線C分別相交于A、B兩點(diǎn)(不同于點(diǎn)O),且
相互垂直,與曲線C分別相交于A、B兩點(diǎn)(不同于點(diǎn)O),且![]() 的傾斜角為銳角
的傾斜角為銳角![]() .
.
(1)求曲線C和射線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)求△OAB的面積的最小值,并求此時![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com