【題目】已知點G（5，4），圓C1：（x﹣1）2+（y﹣4）2=25，過點G的動直線l與圓C1 ， 相交于兩點E、F，線段EF的中點為C． （Ⅰ）求點C的軌跡C2的方程；
（Ⅱ）若過點A（1，0）的直線l1：kx﹣y﹣k=0，與C2相交于兩點P、Q，線段PQ的中點為M，l1與l2：x+2y+2=0的交點為N，求證：|AM||AN|為定值．
【答案】（Ⅰ）解：圓C1：（x﹣1）2+（y﹣4）2=25的圓心C1（1，4），半徑為5，
設C（x，y），由圓的性質及勾股定理，
得（x﹣1）2+（y﹣4）2+（x﹣5）2+（y﹣4）2=（5﹣1）2+（4﹣4）2，
化簡并整理，得（x﹣3）2+（y﹣4）2=4，∴點C的軌跡C2的方程為：（x﹣3）2+（y﹣4）2=4．
（Ⅱ）證明：∵過點A（1，0）的直線l1與C2相交于P、Q兩點．
結合C2的方程（x﹣3）2+（y﹣4）2=4，知k≠0，
解方程組 
，得 
，
有直線C2M與l1垂直，∴C2M的方程為 
，
解 
得， 
，
則 
， 
，
∴ 
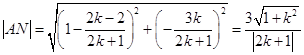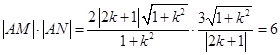為定值
【解析】（Ⅰ）設C（x，y），由圓的性質及勾股定理，得（x﹣1）2+（y﹣4）2+（x﹣5）2+（y﹣4）2=（5﹣1）2+（4﹣4）2，即可求點C的軌跡C2的方程；（Ⅱ）分別聯立相應方程，求得M，N的坐標，再求：|AM||AN|為定值．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1=1，且an=2an﹣1+2n（n≥2，且n∈N*）
（1）求證：數列{ 
}是等差數列；
（2）求數列{an}的通項公式；
（3）設數列{an}的前n項之和Sn ， 求證： 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在奧運會射箭決賽中，參賽號碼為1～4號的4名射箭運動員參加射箭比賽．
（1）通過抽簽將他們安排到1～4號靶位，試求恰有2名運動員所抽靶位號與其參賽號碼相同的概率；
（2）記1號、2號射箭運動員射箭的環數為ξ（ξ所有取值為0，1，2，3，…，10）分別為P1 ， P2 ． 根據教練員提供的資料，其概率分布如下表：
ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
P1 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
P2 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
①若1，2號運動員各射箭一次，求兩人中至少有一人命中9環的概率；
②判斷1號、2號射箭運動員誰射箭的水平高？并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，正方體ABCD﹣A′B′C′D′的棱長為1，E、F分別是棱AA′，CC′的中點，過直線E，F的平面分別與棱BB′、DD′交于M、N，設BM=x，x∈（0，1），給出以下四個命題：
①四邊形MENF為平行四邊形；
②若四邊形MENF面積s=f（x），x∈（0，1），則f（x）有最小值；
③若四棱錐A﹣MENF的體積V=p（x），x∈（0，1），則p（x）為常函數；
④若多面體ABCD﹣MENF的體積V=h（x），x∈（ 
，1），則h（x）為單調函數；
其中假命題為 （ ）
A.①
B.②
C.③
D.④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=a（x+a）（x﹣a+3），g（x）=2x+2﹣1，若對任意x∈R，f（x）＞0和g（x）＞0至少有一個成立，則實數a的取值范圍是（ ）
A.（1，2）
B.（2，3）
C.（﹣2，﹣1）∪（1，+∞）
D.（0，2）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=﹣x2+2|x﹣a|，x∈R．
（1）若函數f（x）為偶函數，求實數a的值；
（2）當x=﹣1時，函數f（x）在x=﹣1取得最大值，求實數a的取值范圍．
（3）若函數f（x）有三個零點，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
