
【題目】設數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)求![]() ;
;
(2)先猜想出![]() 的一個通項公式,再用數學歸納法證明你的猜想.
的一個通項公式,再用數學歸納法證明你的猜想.
【答案】(1)5,7,9;(2)猜想![]() ;證明祥見解析.
;證明祥見解析.
【解析】
試題分析:(1)由已知等式:![]() 令n=1,再將
令n=1,再將![]() 代入即可求得
代入即可求得![]() 的值;再令n=2并將
的值;再令n=2并將![]() 的值就可求得
的值就可求得![]() 的值;最后再令n=2并將
的值;最后再令n=2并將![]() 的值就可求得
的值就可求得![]() 的值;(2)由已知及(1)的結果,可猜想出
的值;(2)由已知及(1)的結果,可猜想出![]() 的一個通項公式;用數學歸納法證明時應注意格式:①驗證
的一個通項公式;用數學歸納法證明時應注意格式:①驗證![]() 時猜想正確;②作歸納假設:假設當
時猜想正確;②作歸納假設:假設當![]() 時,猜想成立,在此基礎上來證明
時,猜想成立,在此基礎上來證明![]() 時猜想也成立,注意在此證明過程中要充分利用已知條件找出
時猜想也成立,注意在此證明過程中要充分利用已知條件找出![]() 之間的關系,并一定要用到假設當
之間的關系,并一定要用到假設當![]() 時的結論;最后一定要下結論.
時的結論;最后一定要下結論.
試題解析: (1)由條件![]() ,依次得
,依次得![]() ,
,
![]() ,
,![]() , 6分
, 6分
(2)由(1),猜想![]() . 7分
. 7分
下用數學歸納法證明之:
①當![]() 時,
時,![]() ,猜想成立; 8分
,猜想成立; 8分
②假設當![]() 時,猜想成立,即有
時,猜想成立,即有![]() , 9分
, 9分
則當![]() 時,有
時,有![]() ,
,
即當![]() 時猜想也成立, 13分
時猜想也成立, 13分
綜合①②知,數列![]() 通項公式為
通項公式為![]() . 14分
. 14分


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】設橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上頂點為
,上頂點為![]() ,過點
,過點![]() 與
與![]() 垂直的直線交
垂直的直線交![]() 軸負半軸于點
軸負半軸于點![]() ,且
,且![]() .
.
(Ⅰ)求橢圓![]() 的離心率;
的離心率;
(Ⅱ)若過![]() 、
、![]() 、
、![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() :
: ![]() 相切,求橢圓
相切,求橢圓![]() 的方程;
的方程;
(III)在(Ⅱ)的條件下,過右焦點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() 使得以
使得以![]() 為鄰邊的平行四邊形是菱形,如果存在,求出
為鄰邊的平行四邊形是菱形,如果存在,求出![]() 的取值范圍,如果不存在,說明理由
的取值范圍,如果不存在,說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=aln(x2+1)+bx存在兩個極值點x1 , x2 .
(1)求證:|x1+x2|>2;
(2)若實數λ滿足等式f(x1)+f(x2)+a+λb=0,試求λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了![]() 至
至![]() 月份每月
月份每月![]() 號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差
|
|
|
|
|
|
|
就診人數 |
|
|
|
|
|
|
該興趣小組確定的研究方案是:先從這六組數據中選取![]() 組,用剩下的
組,用剩下的![]() 組數據求線性回歸方程,再用被選取的
組數據求線性回歸方程,再用被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
(1)求選取的![]() 組數據恰好是相鄰兩月的概率;
組數據恰好是相鄰兩月的概率;
(2)若選取的是1月與![]() 月的兩組數據,請根據2至5月份的數據,求出
月的兩組數據,請根據2至5月份的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過![]() 人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
參考數據![]() ,
,![]()
(參考公式:
 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合![]() ,
,![]() .記
.記![]() 為同時滿足下列條件的集合
為同時滿足下列條件的集合![]() 的個數:
的個數:
①![]() ;②若
;②若![]() ,則
,則![]() ;③若
;③若![]() ,則
,則![]() .
.
則(![]() )
)![]() ___________;
___________;
(![]() )
)![]() 的解析式(用
的解析式(用![]() 表示)
表示)![]() ___________.
___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
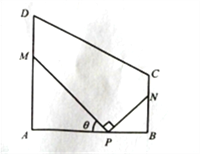
【題目】某地方政府要將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂廣場.已知AD//BC, ![]() 百米,
百米, ![]() 百米,廣場入口P在AB上,且
百米,廣場入口P在AB上,且![]() ,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),
,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),![]() 區域擬建為跳舞健身廣場,
區域擬建為跳舞健身廣場, ![]() 區域擬建為兒童樂園,其它區域鋪設綠化草坪,設
區域擬建為兒童樂園,其它區域鋪設綠化草坪,設![]() .
.
(1)求綠化草坪面積的最大值;
(2)現擬將兩條小路PNM,PN進行不同風格的美化,PM小路的美化費用為每百米1萬元,PN小路的美化費用為每百米2萬元,試確定M,N的位置,使得小路PM,PN的美化總費用最低,并求出最小費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=asinx![]() cos2x+1(a,b∈R).
cos2x+1(a,b∈R).
(1)當a=1,且![]()
![]() 時,求f(x)的值域;
時,求f(x)的值域;
(2)若存在實數![]()
![]() 使得
使得![]() 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
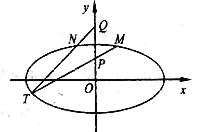
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓
,以原點為圓心,橢圓![]() 的短半軸長為半徑的圓與直線
的短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)已知點![]() ,設
,設![]() 是橢圓
是橢圓![]() 上關于
上關于![]() 軸對稱的不同兩點,直線
軸對稱的不同兩點,直線![]() 與
與![]() 相交于點
相交于點![]() ,求證:點
,求證:點![]() 在橢圓上.
在橢圓上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com