
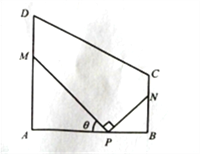
【題目】某地方政府要將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂(lè)廣場(chǎng).已知AD//BC, ![]() 百米,
百米, ![]() 百米,廣場(chǎng)入口P在AB上,且
百米,廣場(chǎng)入口P在AB上,且![]() ,根據(jù)規(guī)劃,過(guò)點(diǎn)P鋪設(shè)兩條相互垂直的筆直小路PM,PN(小路的寬度不計(jì)),點(diǎn)M,N分別在邊AD,BC上(包含端點(diǎn)),
,根據(jù)規(guī)劃,過(guò)點(diǎn)P鋪設(shè)兩條相互垂直的筆直小路PM,PN(小路的寬度不計(jì)),點(diǎn)M,N分別在邊AD,BC上(包含端點(diǎn)),![]() 區(qū)域擬建為跳舞健身廣場(chǎng),
區(qū)域擬建為跳舞健身廣場(chǎng), ![]() 區(qū)域擬建為兒童樂(lè)園,其它區(qū)域鋪設(shè)綠化草坪,設(shè)
區(qū)域擬建為兒童樂(lè)園,其它區(qū)域鋪設(shè)綠化草坪,設(shè)![]() .
.
(1)求綠化草坪面積的最大值;
(2)現(xiàn)擬將兩條小路PNM,PN進(jìn)行不同風(fēng)格的美化,PM小路的美化費(fèi)用為每百米1萬(wàn)元,PN小路的美化費(fèi)用為每百米2萬(wàn)元,試確定M,N的位置,使得小路PM,PN的美化總費(fèi)用最低,并求出最小費(fèi)用.
【答案】(1) 綠化草坪面積的最大值為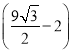 平方百米;(2)
平方百米;(2) ![]() 時(shí)總美化費(fèi)用最低為4萬(wàn)元.
時(shí)總美化費(fèi)用最低為4萬(wàn)元.
【解析】試題分析:(1)先求得![]()
![]() ,再利用均值不等式求得正解;(2)先求得
,再利用均值不等式求得正解;(2)先求得![]() ,
, ![]()
總美化費(fèi)用為![]() ,再利用導(dǎo)數(shù)工具求得正解.
,再利用導(dǎo)數(shù)工具求得正解.
試題解析:(1)在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以![]()
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以![]()
所以綠化草坪面積![]()
![]()
![]()
![]()
又因?yàn)?/span>![]()
當(dāng)且當(dāng)![]() ,即
,即![]() 。此時(shí)
。此時(shí)![]()
所以綠化草坪面積的最大值為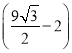 平方百米.
平方百米.
(2)方法一:在![]() 中,
中, ![]() ,得
,得![]() ,
,
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以總美化費(fèi)用為![]()
![]()
![]()
令![]() 得
得![]() 列表如下
列表如下
|
|
|
|
|
|
| - | 0 | - | ||
|
| 單調(diào)遞減 |
| 單調(diào)遞增 |
|
所以當(dāng)![]() 時(shí),即
時(shí),即![]() 時(shí)總美化費(fèi)用最低為4萬(wàn)元。
時(shí)總美化費(fèi)用最低為4萬(wàn)元。
方法二:在![]() 中,
中, ![]() ,得
,得![]() ,
,
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以總美化費(fèi)用為![]()
![]()
令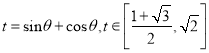 得
得![]()
所以![]() ,
, 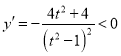
所以![]() 在
在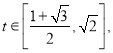 上是單調(diào)遞減
上是單調(diào)遞減
所以當(dāng)![]() ,
, ![]() 時(shí),即
時(shí),即![]() 時(shí)總美化費(fèi)用最低為4萬(wàn)元。
時(shí)總美化費(fèi)用最低為4萬(wàn)元。


 一諾書業(yè)暑假作業(yè)快樂(lè)假期云南美術(shù)出版社系列答案
一諾書業(yè)暑假作業(yè)快樂(lè)假期云南美術(shù)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() 的內(nèi)角A,B,C的對(duì)邊分別為a,b,c,
的內(nèi)角A,B,C的對(duì)邊分別為a,b,c,![]() ,且B為鈍角,
,且B為鈍角,
(1)![]() ;(2)求
;(2)求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
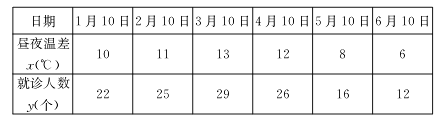
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數(shù)多少之間的關(guān)系,他們分別到氣象局與某醫(yī)院抄錄了1至6月每月10號(hào)的晝夜溫差情況與因患感冒而就診的人數(shù),得到如下的資料:
該興趣小組確定的研究方案是:現(xiàn)從這六組數(shù)據(jù)中選取2組,用剩下的4組數(shù)據(jù)求線性回歸方程,再用被選用的2組數(shù)據(jù)進(jìn)行檢驗(yàn).
(1)求選取的2組數(shù)據(jù)恰好是相鄰兩個(gè)月的概率;
(2)若選取的是1月與6月的兩組數(shù)據(jù),請(qǐng)根據(jù)2至5月的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若有線性回歸方程得到的估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過(guò)2人,則認(rèn)為得到的線性回歸方程是理想的,試問(wèn)(2)中所得線性回歸方程是否是理想?
參考公式:
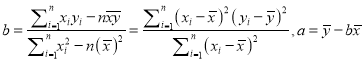
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若定義在![]() 上的函數(shù)
上的函數(shù)![]() ,其圖象是連續(xù)不斷的,且存在常數(shù)
,其圖象是連續(xù)不斷的,且存在常數(shù)![]() 使得
使得![]() 對(duì)任意的實(shí)數(shù)
對(duì)任意的實(shí)數(shù)![]() 都成立,則稱
都成立,則稱![]() 是一個(gè)“
是一個(gè)“![]() 特征函數(shù)”則下列結(jié)論中正確的個(gè)數(shù)為( ).
特征函數(shù)”則下列結(jié)論中正確的個(gè)數(shù)為( ).
①![]() 是常數(shù)函數(shù)中唯一的“
是常數(shù)函數(shù)中唯一的“![]() 特征函數(shù)”;
特征函數(shù)”;
②![]() 不是“
不是“![]() 特征函數(shù)”;
特征函數(shù)”;
③“![]() 特征函數(shù)”至少有一個(gè)零點(diǎn);
特征函數(shù)”至少有一個(gè)零點(diǎn);
④![]() 是一個(gè)“
是一個(gè)“![]() 特征函數(shù)”;.
特征函數(shù)”;.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)數(shù)列![]() 滿足
滿足![]() ,
,![]() .
.
(1)求![]() ;
;
(2)先猜想出![]() 的一個(gè)通項(xiàng)公式,再用數(shù)學(xué)歸納法證明你的猜想.
的一個(gè)通項(xiàng)公式,再用數(shù)學(xué)歸納法證明你的猜想.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若對(duì)![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)當(dāng)![]() 時(shí),求
時(shí),求![]() 在
在![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線l1的方程為3x+4y﹣12=0.
(1)若直線l2與l1平行,且過(guò)點(diǎn)(﹣1,3),求直線l2的方程;
(2)若直線l2與l1垂直,且l2與兩坐標(biāo)軸圍成的三角形面積為4,求直線l2的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】桑基魚塘是某地一種獨(dú)具地方特色的農(nóng)業(yè)生產(chǎn)形式,某研究單位打算開(kāi)發(fā)一個(gè)桑基魚塘項(xiàng)目,該項(xiàng)目準(zhǔn)備購(gòu)置一塊![]() 平方米的矩形地塊,中間挖成三個(gè)矩形池塘養(yǎng)魚,挖出的泥土堆在池塘四周形成基圍(陰影部分所示)種植桑樹(shù),池塘周圍的基圍寬均為
平方米的矩形地塊,中間挖成三個(gè)矩形池塘養(yǎng)魚,挖出的泥土堆在池塘四周形成基圍(陰影部分所示)種植桑樹(shù),池塘周圍的基圍寬均為![]() 米,如圖,設(shè)池塘所占總面積為
米,如圖,設(shè)池塘所占總面積為![]() 平方米.
平方米.
(Ⅰ)試用![]() 表示
表示![]() .
.
(Ⅱ)當(dāng)![]() 取何值時(shí),才能使得
取何值時(shí),才能使得![]() 最大?并求出
最大?并求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]()
(1)若函數(shù)![]() 在定義域內(nèi)單調(diào)遞增,求實(shí)數(shù)
在定義域內(nèi)單調(diào)遞增,求實(shí)數(shù) ![]() 的取值范圍,
的取值范圍,
(2)當(dāng)![]() 時(shí),關(guān)于
時(shí),關(guān)于![]() 的方程
的方程![]() 在[1,4]上恰有兩個(gè)不相等的實(shí)數(shù)根,
在[1,4]上恰有兩個(gè)不相等的實(shí)數(shù)根,
求實(shí)數(shù)的取值范圍。
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com