
設函數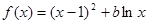 ,其中
,其中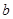 為常數。
為常數。
(Ⅰ)當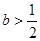 時,判斷函數
時,判斷函數 在定義域上的單調性;
在定義域上的單調性;
(Ⅱ)若函數 有極值點,求
有極值點,求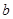 的取值范圍及
的取值范圍及 的極值點。
的極值點。
(Ⅰ)函數 在定義域
在定義域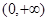 上單調遞增;(Ⅱ)當且僅當
上單調遞增;(Ⅱ)當且僅當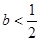 時
時 有極值點;當
有極值點;當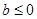 時,
時, 有惟一最小值點
有惟一最小值點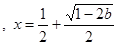 ;當
;當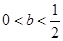 時,
時, 有一個極大值點
有一個極大值點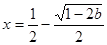 和一個極小值點
和一個極小值點 .
.
解析試題分析:(Ⅰ)函數 在定義域上的單調性的方法,一是利用定義,二是利用導數,此題既有代數函數又有對數函數,顯然利用導數判斷,只需對
在定義域上的單調性的方法,一是利用定義,二是利用導數,此題既有代數函數又有對數函數,顯然利用導數判斷,只需對 求導,判斷
求導,判斷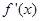 的符號即可;(Ⅱ)求
的符號即可;(Ⅱ)求 的極值,只需對
的極值,只需對 求導即可,利用導數求函數的極值一般分為四個步驟:①確定函數的定義域;②求出
求導即可,利用導數求函數的極值一般分為四個步驟:①確定函數的定義域;②求出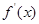 ;③令
;③令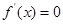 ,列表;④確定函數的極值.此題由(Ⅰ)得,當
,列表;④確定函數的極值.此題由(Ⅰ)得,當 時,函數
時,函數 無極值點,只需討論
無極值點,只需討論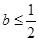 的情況,解
的情況,解 的根,討論在
的根,討論在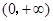 范圍內根的個數,從而確定
范圍內根的個數,從而確定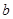 的取值范圍及
的取值范圍及 的極值點,值得注意的是,求出
的極值點,值得注意的是,求出 的根時,忽略討論根是否在定義域內,而出錯.
的根時,忽略討論根是否在定義域內,而出錯.
試題解析:(Ⅰ)由題意知, 的定義域為
的定義域為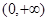 ,
,
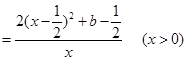 ∴當
∴當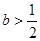 時,
時,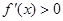 ,函數
,函數 在定義域
在定義域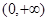 上單調遞增.
上單調遞增.
(Ⅱ)①由(Ⅰ)得,當 時,函數
時,函數 無極值點,②
無極值點,②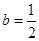 時,
時,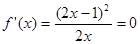 有兩個相同的解
有兩個相同的解 ,但當
,但當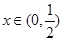 時,
時,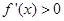 ,當
,當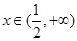 時,
時,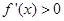
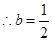 時,函數
時,函數 在
在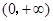 上無極值點,③當
上無極值點,③當 時,
時, 有兩個不同解,
有兩個不同解,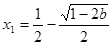
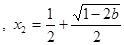 ,
, 時,
時, ,而
,而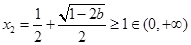 ,此時
,此時 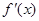 ,
, 隨
隨 在定義域上的變化情況如下表:
在定義域上的變化情況如下表: