解:(1)∵f(x)=
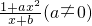
是奇函數,
∴f(-x)+f(x)=
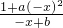
+

=(1+ax
2)•
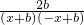
=0,
∴b=0;
∴f(x)=
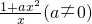
,又f(x)的圖象經過點(1,3),
∴
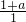
=3,
∴a=2;
∴f(x)=2x+

;
(2)當x>0時,f(x)=2x+

在[

,+∞)上單調遞增.
證明:令

≤x
1<x
2,
則f(x
2)-f(x
1)=2(x
2-x
1)+(

-

)=(x
2-x
1)(2-
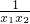
),
∵

≤x
1<x
2,
∴0<
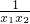
<2,于是2-
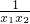
>0,
∴(x
2-x
1)(2-
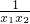
)>0,
∴f(x
2)>f(x
1).
∴當x>0時,f(x)=2x+

在[

,+∞)上單調遞增.
(3)∵f(x)=2x+

(x>0),
∴f′(x)=2-

,由f′(x)≥0可得x≥

,由f′(x)<0可得0<x<

,
∴f(x)=2x+

在[

,+∞)上單調遞增,在(0,

]上單調遞減.
∴f(x)=2x+

在x=

處取到最小值2

,
∴當x>0時f(x)=2x+

的值域為:[2

,+∞).
分析:(1)由f(-x)+f(x)=0可求得b=0;又f(x)的圖象經過點(1,3),從而可求得a;
(2)當x>0時,f(x)=2x+

在[

,+∞)上單調遞增,利用單調性的定義證明即可;
(3)可利用導數判斷f(x)=2x+

在[

,+∞)上單調遞增,在(0,

]上單調遞減,從而可確定函數f(x)當x>0時的值域.
點評:本題考查函數奇偶性與單調性的綜合,難點在于函數單調增區間的確定(導數法先判斷,再用定義證明),著重考查函數奇偶性與單調性的性質及其應用,綜合性強,屬于難題.

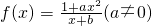 是奇函數,并且函數f(x)的圖象經過點(1,3)
是奇函數,并且函數f(x)的圖象經過點(1,3)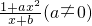 是奇函數,
是奇函數,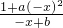 +
+ =(1+ax2)•
=(1+ax2)•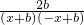 =0,
=0,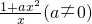 ,又f(x)的圖象經過點(1,3),
,又f(x)的圖象經過點(1,3),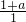 =3,
=3, ;
; 在[
在[ ,+∞)上單調遞增.
,+∞)上單調遞增. ≤x1<x2,
≤x1<x2, -
- )=(x2-x1)(2-
)=(x2-x1)(2-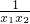 ),
), ≤x1<x2,
≤x1<x2,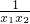 <2,于是2-
<2,于是2-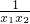 >0,
>0,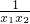 )>0,
)>0, 在[
在[ ,+∞)上單調遞增.
,+∞)上單調遞增. (x>0),
(x>0), ,由f′(x)≥0可得x≥
,由f′(x)≥0可得x≥ ,由f′(x)<0可得0<x<
,由f′(x)<0可得0<x< ,
, 在[
在[ ,+∞)上單調遞增,在(0,
,+∞)上單調遞增,在(0, ]上單調遞減.
]上單調遞減. 在x=
在x= 處取到最小值2
處取到最小值2 ,
, 的值域為:[2
的值域為:[2 ,+∞).
,+∞). 在[
在[ ,+∞)上單調遞增,利用單調性的定義證明即可;
,+∞)上單調遞增,利用單調性的定義證明即可; 在[
在[ ,+∞)上單調遞增,在(0,
,+∞)上單調遞增,在(0, ]上單調遞減,從而可確定函數f(x)當x>0時的值域.
]上單調遞減,從而可確定函數f(x)當x>0時的值域.

 是奇函數,并且函數f(x)的圖象經過點(1,3),
是奇函數,并且函數f(x)的圖象經過點(1,3),