
【題目】某種產(chǎn)品的質(zhì)量以其質(zhì)量指標值來衡量,質(zhì)量指標值越大表明質(zhì)量越好,記其質(zhì)量指標值為![]() ,當
,當![]() 時,產(chǎn)品為一級品;當
時,產(chǎn)品為一級品;當![]() 時,產(chǎn)品為二級品,當
時,產(chǎn)品為二級品,當![]() 時,產(chǎn)品為三級品,現(xiàn)用兩種新配方(分別稱為
時,產(chǎn)品為三級品,現(xiàn)用兩種新配方(分別稱為![]() 配方和
配方和![]() 配方)做實驗,各生產(chǎn)了
配方)做實驗,各生產(chǎn)了![]() 件這種產(chǎn)品,并測量了每件產(chǎn)品的質(zhì)量指標值,得到下面的試驗結(jié)果 :(以下均視頻率為概率)
件這種產(chǎn)品,并測量了每件產(chǎn)品的質(zhì)量指標值,得到下面的試驗結(jié)果 :(以下均視頻率為概率)
![]() 配方的頻數(shù)分配表:
配方的頻數(shù)分配表:
指標值分組 |
|
|
|
|
頻數(shù) |
|
|
|
|
![]() 配方的頻數(shù)分配表:
配方的頻數(shù)分配表:
指標值分組 |
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
(1)若從![]() 配方產(chǎn)品中有放回地隨機抽取
配方產(chǎn)品中有放回地隨機抽取![]() 件,記“抽出的
件,記“抽出的![]() 配方產(chǎn)品中至少
配方產(chǎn)品中至少![]() 件二級品”為事件
件二級品”為事件![]() ,求事件
,求事件![]() 發(fā)生的概率
發(fā)生的概率![]() ;
;
(2)若兩種新產(chǎn)品的利潤率![]() 與質(zhì)量指標
與質(zhì)量指標![]() 滿足如下關(guān)系:
滿足如下關(guān)系: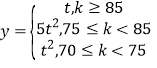 ,其中
,其中![]() ,從長期來看,投資哪種配方的產(chǎn)品平均利潤率較大?
,從長期來看,投資哪種配方的產(chǎn)品平均利潤率較大?
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)等差數(shù)列![]() 滿足
滿足![]() ,
,![]() ,
,
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)求![]() 的最大項的值;
的最大項的值;
(3)數(shù)列![]() 滿足
滿足![]() ,問是否存在正整數(shù)k,使得
,問是否存在正整數(shù)k,使得![]()
![]() 成等差數(shù)列?若存在,求出k和m的值;若不存在,請說明理由.
成等差數(shù)列?若存在,求出k和m的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“珠算之父”程大位是我國明代著名的數(shù)學(xué)家,他的應(yīng)用巨著《算法統(tǒng)綜》中有一首“竹筒容米”問題:“家有九節(jié)竹一莖,為因盛米不均平,下頭三節(jié)四升五,上梢四節(jié)三升八,唯有中間兩節(jié)竹,要將米數(shù)次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容積依次相差同一數(shù)量.)用你所學(xué)的數(shù)學(xué)知識求得中間兩節(jié)竹的容積為
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知P是曲線![]() 上的點,Q是曲線
上的點,Q是曲線![]() 上的點,曲線
上的點,曲線![]() 與曲線
與曲線![]() 關(guān)于直線
關(guān)于直線![]() 對稱,M為線段PQ的中點,O為坐標原點,則
對稱,M為線段PQ的中點,O為坐標原點,則![]() 的最小值為________.
的最小值為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為4的正方形,
是邊長為4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是線段
是線段![]() 上一點,求三棱錐
上一點,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知:在平面四邊形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如圖1),若將
(如圖1),若將![]() 沿對角線BD折疊,使
沿對角線BD折疊,使![]() (如圖2).請在圖2中解答下列問題.
(如圖2).請在圖2中解答下列問題.
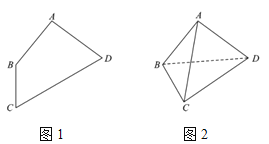
(1)證明:![]() ;
;
(2)求三棱錐![]() 的高.
的高.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 和曲線
和曲線![]() 的極坐標方程;
的極坐標方程;
(2)已知射線![]() (
(![]() ),將射線
),將射線![]() 順時針方向旋轉(zhuǎn)
順時針方向旋轉(zhuǎn)![]() 得到
得到![]() :
:![]() ,且射線
,且射線![]() 與曲線
與曲線![]() 交于兩點,射線
交于兩點,射線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=sin(x+![]() )+sin(x﹣
)+sin(x﹣![]() )+cosx.
)+cosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)在△ABC中,f(A)=![]() ,△ABC的面積為
,△ABC的面積為![]() ,AB=
,AB=![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】[選修4-4:坐標系與參數(shù)方程]:在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() ,
,![]() 的直角坐標方程;
的直角坐標方程;
(2)判斷曲線![]() ,
,![]() 是否相交,若相交,請求出交點間的距離;若不相交,請說明理由.
是否相交,若相交,請求出交點間的距離;若不相交,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com