
����С�}�M��12�֣��c(di��n)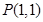 ��E�A
��E�A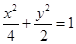 ��(n��i)��һ���c(di��n)���^(gu��)P�c(di��n)��һֱ�����c�E�A�ཻ��
��(n��i)��һ���c(di��n)���^(gu��)P�c(di��n)��һֱ�����c�E�A�ཻ��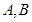 ���c(di��n)����Pǡ�Þ���AB�����c(di��n)����D��ʾ������AB���ڵ�ֱ�����̼���AB���L(zh��ng)�ȡ�
���c(di��n)����Pǡ�Þ���AB�����c(di��n)����D��ʾ������AB���ڵ�ֱ�����̼���AB���L(zh��ng)�ȡ�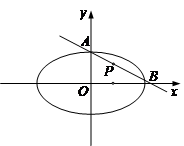
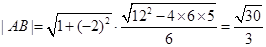 ��
��
����ԇ�}����������A��B���c(di��n)��ֱ���c�E�A�Ľ��c(di��n)����������(y��ng)�M��E�A���̣��O(sh��)������������(bi��o)��Ȼ�����(j��)���������c(di��n)��M���Ɍ�����(bi��o)�g���P(gu��n)ϵ�D(zhu��n)������ֱ��l��б�ʣ�Ȼ�������c(di��n)бʽ���ֱ�����̣����Ã��c(di��n)���x��ʽ�õ��ҵ��L(zh��ng)�ȵ���⡣
�⣺�O(sh��)ֱ���c�E�A����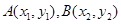 ���t
���t ������
������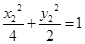 ����
����
��-�ٵ�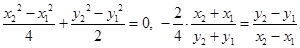 ����
����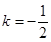 ��
��
������ֱ�����̞飺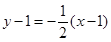 ����
����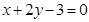 ��
��
�������E�A���������ã�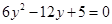 ������(j��)���L(zh��ng)��ʽ��
������(j��)���L(zh��ng)��ʽ�� ��
��
���c(di��n)�����}��Ҫ����ֱ���c�E�A��λ���P(gu��n)ϵ���\(y��n)�á�
�c(di��n)�u(p��ng)����Qԓԇ�}���P(gu��n)�I����ֱ�����̕r(sh��)����(y��ng)���x���m��(d��ng)?sh��)�ֱ�����̵���ʽ����ע����N��ʽ���m�×l������б��ʽ���c(di��n)бʽ�r(sh��)��ֱ����б�ʱ�횴��ڣ������c(di��n)ʽ���ܱ�ʾ�c����(bi��o)�S��ֱ��ֱ�����ؾ�ʽ���ܱ�ʾ�c����(bi��o)�S��ֱ��(j��ng)�^(gu��)ԭ�c(di��n)��ֱ�������ڽ��}�r(sh��)�������ýؾ�ʽ����(y��ng)ע����(l��i)ӑՓ���Д�ؾ��Ƿ���㣻�������c(di��n)бʽ����(y��ng)�ȿ��]б�ʲ����ڵ���r��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
(���}�M��14��)
��֪�E�A
 ,�����(zh��n)����
,�����(zh��n)���� ���Ҝ�(zh��n)����
���Ҝ�(zh��n)���� �����タ
�����タ ������(bi��o)ԭ�c(di��n)
������(bi��o)ԭ�c(di��n) ����c(di��n)��
����c(di��n)�� ���(zh��n)����
���(zh��n)���� ��
�� ��
�� ���c(di��n).
���c(di��n).
��1�����タ �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���� ���L(zh��ng)��.
���L(zh��ng)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪���タ �^(gu��)�c(di��n)
�^(gu��)�c(di��n) ��
��
��I�����タ�ķ��̣�
��II����֪�A���� �S�ϵĈA
�S�ϵĈA �^(gu��)�c(di��n)
�^(gu��)�c(di��n) ���҈A
���҈A ���c(di��n)
���c(di��n) ���о�ǡ�ǒ��タ���c(di��n)
���о�ǡ�ǒ��タ���c(di��n) ���о�����A
���о�����A �ķ��̣�
�ķ��̣�
������D���c(di��n) ��
�� �S��һ�c(di��n)���c(di��n)
�S��һ�c(di��n)���c(di��n) ���c(di��n)
���c(di��n) �P(gu��n)��ԭ�c(di��n)�Č�(du��)�Q(ch��ng)�c(di��n)���^(gu��)�c(di��n)
�P(gu��n)��ԭ�c(di��n)�Č�(du��)�Q(ch��ng)�c(di��n)���^(gu��)�c(di��n) ��һ�lֱ���c���タ����
��һ�lֱ���c���タ���� ���c(di��n)����
���c(di��n)���� ���C��:
���C��: ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
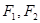 �քe�ǙE�A
�քe�ǙE�A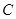 ��
��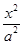 +
+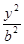 =1��
=1��
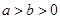 �������ҽ��c(di��n)��
�������ҽ��c(di��n)��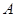 �ǙE�A
�ǙE�A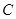 ������c(di��n)��
������c(di��n)��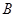 ��ֱ��
��ֱ��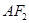 �c�E�A
�c�E�A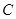 ����һ��(g��)���c(di��n)��
����һ��(g��)���c(di��n)��
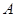
 =60��.
=60��.
��1����E�A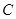 ���x���ʣ�
���x���ʣ�
��2����֪��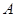
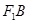 ����e��40
����e��40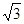 ����a, b ��ֵ.
����a, b ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
(��С�}12��)�O(sh��) ,��ƽ��ֱ������(bi��o)ϵ��,��֪����
,��ƽ��ֱ������(bi��o)ϵ��,��֪���� ,����
,���� ,
, ,��(d��ng)�c(di��n)
,��(d��ng)�c(di��n) ��܉�E��E. ��܉�EE�ķ���,���f(shu��)��ԓ��������ʾ�������Π
��܉�E��E. ��܉�EE�ķ���,���f(shu��)��ԓ��������ʾ�������Π
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��12�֣���֪���タ ��
��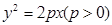 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)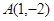 .��1�����タ
.��1�����タ �ķ��̣��������(zh��n)�����̣�
�ķ��̣��������(zh��n)�����̣�
��2���Ƿ����ƽ����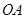 ��
�� ������(bi��o)ԭ�c(di��n)����ֱ��
������(bi��o)ԭ�c(di��n)����ֱ��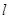 ��ʹ��ֱ��
��ʹ��ֱ��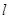 �c���タ
�c���タ �й����c(di��n)����ֱ��
�й����c(di��n)����ֱ��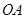 �c
�c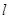 ��
��
���x����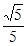 �������ڣ����ֱ��
�������ڣ����ֱ��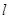 �ķ��̣��������ڣ��f(shu��)������.
�ķ��̣��������ڣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�c(di��n)P�LjA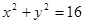 �ϵ�һ��(g��)��(d��ng)�c(di��n)���^(gu��)�c(di��n)P��PD��ֱ��
�ϵ�һ��(g��)��(d��ng)�c(di��n)���^(gu��)�c(di��n)P��PD��ֱ�� �S�������D��Q�龀��PD�����c(di��n)��
�S�������D��Q�龀��PD�����c(di��n)��
��1�����c(di��n)Q��܉�E���̡�
��2����֪�c(di��n)M��1��1�����������̵ĈD��(n��i)һ�c(di��n)���^(gu��)�c(di��n)M����AB�����c(di��n)Mǡ����AB�����c(di��n)����ֱ��AB�ķ��̡�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��12�֣���֪�E�A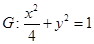 ���^(gu��)�c(di��n)��m,0�����A
���^(gu��)�c(di��n)��m,0�����A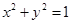 ���о�
���о�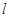 ���E�AG��A��B���c(di��n).
���E�AG��A��B���c(di��n).
��1����E�AG�Ľ��c(di��n)����(bi��o)���x���ʣ�
��2����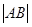 ��ʾ��m�ĺ���(sh��)������
��ʾ��m�ĺ���(sh��)������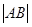 �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
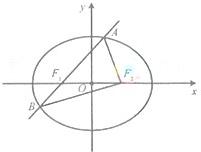
�����}�M��14��)��D���E�A ��
��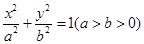 �����c(di��n)��
�����c(di��n)��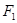 ���ҽ��c(di��n)��
���ҽ��c(di��n)��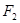 ���x����
���x����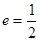 ���^(gu��)
���^(gu��)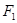 ��ֱ�����E�A��
��ֱ�����E�A�� ���c(di��n)���ҡ�
���c(di��n)���ҡ� �����L(zh��ng)��
�����L(zh��ng)��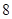 ��
��
������E�A �ķ��̣�
�ķ��̣�
�����O(sh��)��(d��ng)ֱ��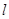 ��
��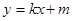 �c�E�A
�c�E�A ����ֻ��һ��(g��)�����c(di��n)
����ֻ��һ��(g��)�����c(di��n)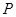 �����cֱ��
�����cֱ��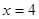 �ཻ���c(di��n)
�ཻ���c(di��n)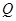 ��ԇ̽����������(bi��o)ƽ���(n��i)�Ƿ���ڶ��c(di��n)
��ԇ̽����������(bi��o)ƽ���(n��i)�Ƿ���ڶ��c(di��n)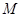 ��ʹ����
��ʹ����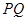 ��ֱ���ĈA���^(gu��)�c(di��n)
��ֱ���ĈA���^(gu��)�c(di��n)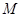 �������ڣ�����c(di��n)
�������ڣ�����c(di��n)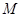 ������(bi��o)���������ڣ��f(shu��)�����ɣ�
������(bi��o)���������ڣ��f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com