
【題目】設函數![]() .
.
(1)若函數![]() 在區間
在區間![]() (
(![]() 為自然對數的底數)上有唯一的零點,求實數
為自然對數的底數)上有唯一的零點,求實數![]() 的取值范圍;
的取值范圍;
(2)若在![]() (
(![]() 為自然對數的底數)上存在一點
為自然對數的底數)上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 或
或![]() (2)
(2)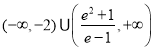 .
.
【解析】
(1)求得![]() ,對
,對![]() 的范圍分類,即可判斷函數
的范圍分類,即可判斷函數![]() 的單調性,結合
的單調性,結合![]() 即可判斷函數
即可判斷函數![]() 在區間
在區間![]() 上是否有唯一的零點,問題得解。
上是否有唯一的零點,問題得解。
(2)將問題轉化為:函數![]() 在
在![]() 上的最小值小于零.求得
上的最小值小于零.求得![]() ,對
,對![]() 的范圍分類即可判斷函數的單調性,從而求得
的范圍分類即可判斷函數的單調性,從而求得![]() 的最小值,問題得解。
的最小值,問題得解。
(1)![]() ,其中
,其中![]() .
.
①當![]() 時,
時,![]() 恒成立,
恒成立,![]() 單調遞增,
單調遞增,
又∵![]() ,函數
,函數![]() 在區間
在區間![]() 上有唯一的零點,符合題意.
上有唯一的零點,符合題意.
②當![]() 時,
時,![]() 恒成立,
恒成立,![]() 單調遞減,
單調遞減,
又∵![]() ,函數
,函數![]() 在區間
在區間![]() 上有唯一的零點,符合題意.
上有唯一的零點,符合題意.
③當![]() 時,
時,![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
又∵![]() ,∴
,∴![]() ,
,
∴函數![]() 在區間
在區間![]() 有唯一的零點,
有唯一的零點,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
當![]() 時符合題意,即
時符合題意,即![]() ,
,
∴![]() 時,函數
時,函數![]() 在區間
在區間![]() 上有唯一的零點;
上有唯一的零點;
∴![]() 的取值范圍是
的取值范圍是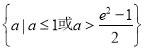 .
.
(2)在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,等價于
成立,等價于![]() 在
在![]() 上有解,即函數
上有解,即函數![]() 在
在![]() 上的最小值小于零.
上的最小值小于零.
![]() ,
,
①當![]() 時,即
時,即![]() 時,
時,![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() 的最小值為
的最小值為![]() ,由
,由![]() 可得
可得![]() ,∵
,∵![]() ,∴
,∴![]() ;
;
②當![]() 時,即
時,即![]() 時,
時,![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() 的最小值為
的最小值為![]() ,由
,由![]() 可得
可得![]() ;
;
③當![]() 時,即
時,即![]() 時,
時,
可得![]() 的最小值為
的最小值為![]() ,∵
,∵![]() ,∴
,∴![]() ,
,![]() ,所以
,所以![]() 不成立.
不成立.
綜上所述:可得所求![]() 的取值范圍是
的取值范圍是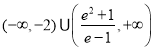 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某公司為了變廢為寶,節約資源,新上了一個從生活垃圾中提煉生物柴油的項目.經測算該項目月處理成本![]() (元)與月處理量
(元)與月處理量![]() (噸)之間的函數關系可以近似地表示為:
(噸)之間的函數關系可以近似地表示為:
 ,且每處理一噸生活垃圾,可得到能利用的生物柴油價值為200元,若該項目不獲利,政府將給予補貼.
,且每處理一噸生活垃圾,可得到能利用的生物柴油價值為200元,若該項目不獲利,政府將給予補貼.
(1)當![]() 時,判斷該項目能否獲利?如果獲利,求出最大利潤;如果不獲利,則政府每月至少需要補貼多少元才能使該項目不虧損?
時,判斷該項目能否獲利?如果獲利,求出最大利潤;如果不獲利,則政府每月至少需要補貼多少元才能使該項目不虧損?
(2)該項目每月處理量為多少噸時,才能使每噸的平均處理成本最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】朱世杰是元代著名數學家,他所著《算學啟蒙》是一部在中國乃至世界最早的科學普及著作.《算學啟蒙》中提到一些堆垛問題,如“三角垛果子”,就是將一樣大小的果子堆垛成正三棱錐,每層皆堆成正三角形,從上向下數,每層果子數分別為1,3,6,10,…,現有一個“三角垛果子”,其最底層每邊果子數為10,則該層果子數為( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 與x軸交于A,B兩點,點Q的坐標為
與x軸交于A,B兩點,點Q的坐標為![]() .
.
(1)是否存在b,使得![]() ,如果存在求出b值;如果不存在,說明理由;
,如果存在求出b值;如果不存在,說明理由;
(2)過A,B,Q三點的圓面積最小時,求圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲、乙兩種產品,已知生產每噸甲產品要用A原料3噸,B原料2噸;生產每噸乙產品要用A原料1噸,B原料3噸.銷售每噸甲產品可獲得利潤5萬元,每噸乙產品可獲得利潤3萬元.該企業在一個生產周期內消耗A原料不超過13噸,B原料不超過18噸.
(1)列出甲、乙兩種產品滿足的關系式,并畫出相應的平面區域;
(2)在一個生產周期內該企業生產甲、乙兩種產品各多少噸時可獲得利潤最大,最大利潤是多少?
(用線性規劃求解要畫出規范的圖形及具體的解答過程)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表,即楊輝三角,這是數學史上的一個偉大成就,在“楊輝三角”中,第![]() 行的所有數字之和為
行的所有數字之和為![]() ,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前15項和為( )
,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前15項和為( )
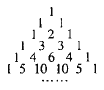
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過原點的直線與橢圓![]() 交于
交于![]() 兩點(
兩點(![]() 不是橢圓
不是橢圓![]() 的頂點),點
的頂點),點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() ,直線
,直線![]() 與
與![]() 軸
軸![]() 軸分別交于
軸分別交于![]() 兩點.
兩點.
①設直線![]() 斜率分別為
斜率分別為![]() ,證明存在常數
,證明存在常數![]() 使得
使得![]() ,并求出
,并求出![]() 的值;
的值;
②求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校學生社團組織活動豐富,學生會為了解同學對社團活動的滿意程度,隨機選取了100位同學進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6組,制成如圖所示頻率分布直方圖.
(1)求圖中x的值;
(2)求這組數據的中位數;
(3)現從被調查的問卷滿意度評分值在[60,80)的學生中按分層抽樣的方法抽取5人進行座談了解,再從這5人中隨機抽取2人作主題發言,求抽取的2人恰在同一組的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com