
【題目】在平面直角坐標(biāo)系![]() 中,橢圓
中,橢圓![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過原點的直線與橢圓![]() 交于
交于![]() 兩點(
兩點(![]() 不是橢圓
不是橢圓![]() 的頂點),點
的頂點),點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() ,直線
,直線![]() 與
與![]() 軸
軸![]() 軸分別交于
軸分別交于![]() 兩點.
兩點.
①設(shè)直線![]() 斜率分別為
斜率分別為![]() ,證明存在常數(shù)
,證明存在常數(shù)![]() 使得
使得![]() ,并求出
,并求出![]() 的值;
的值;
②求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() .
.
(2) ①證明見解析,![]() ;②
;②![]() .
.
【解析】試題分析:(1)首先由題意得到![]() ,即
,即![]() .
.
將![]() 代入
代入![]() 可得
可得![]() ,
,
由![]() ,可得
,可得![]() .
.![]() 得解.
得解.
(2)(ⅰ)注意從確定![]() 的表達式入手,探求使
的表達式入手,探求使![]() 成立的
成立的![]() .
.
設(shè)![]() ,則
,則![]() ,
,
得到![]() ,
,
根據(jù)直線BD的方程為![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() .得到
.得到![]() .
.
由![]() ,作出結(jié)論.
,作出結(jié)論.
(ⅱ)直線BD的方程![]() ,
,
從確定![]() 的面積表達式
的面積表達式![]() 入手,應(yīng)用基本不等式得解.
入手,應(yīng)用基本不等式得解.
試題解析:(1)由題意知![]() ,可得
,可得![]() .
.
橢圓C的方程可化簡為![]() .
.
將![]() 代入可得
代入可得![]() ,
,
因此![]() ,可得
,可得![]() .
.
因此![]() ,
,
所以橢圓C的方程為![]() .
.
(2)(ⅰ)設(shè)![]() ,則
,則![]() ,
,
因為直線AB的斜率![]() ,
,
又![]() ,所以直線AD的斜率
,所以直線AD的斜率![]() ,
,
設(shè)直線AD的方程為![]() ,
,
由題意知![]() ,
,
由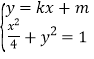 ,可得
,可得![]() .
.
所以![]() ,
,
因此![]() ,
,
由題意知,![]()
所以![]() ,
,
所以直線BD的方程為![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() .
.
可得![]() .
.
所以![]() ,即
,即![]() .
.
因此存在常數(shù)![]() 使得結(jié)論成立.
使得結(jié)論成立.
(ⅱ)直線BD的方程![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,
,
由(ⅰ)知![]() ,
,
可得![]() 的面積
的面積![]() ,
,
因為![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 時等號成立,
時等號成立,
此時S取得最大值![]() ,
,
所以![]() 的面積的最大值為
的面積的最大值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】銷售甲乙兩種商品所得利潤分別是![]() (單位:萬元)和
(單位:萬元)和![]() (單位:萬元),它們與投入資金
(單位:萬元),它們與投入資金![]() (單位:萬元)的關(guān)系有經(jīng)驗公式
(單位:萬元)的關(guān)系有經(jīng)驗公式![]() ,
,![]() .今將10萬元資金投入經(jīng)營甲乙兩種商品,其中對甲種商品投資
.今將10萬元資金投入經(jīng)營甲乙兩種商品,其中對甲種商品投資![]() (單位:萬元).
(單位:萬元).
(1)試建立總利潤![]() (單位:萬元)關(guān)于
(單位:萬元)關(guān)于![]() 的函數(shù)關(guān)系式,并寫出定義域;
的函數(shù)關(guān)系式,并寫出定義域;
(2)如何投資經(jīng)營甲乙兩種商品,才能使得總利潤最大,并求出最大總利潤.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)證明:曲線![]() 上任一點處的切線與直線
上任一點處的切線與直線![]() 和直線
和直線![]() 所圍成的三角形的面積為定值,并求此定值.
所圍成的三角形的面積為定值,并求此定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的一段圖象如圖所示.
的一段圖象如圖所示.
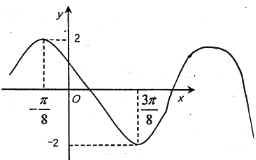
(1)求該函數(shù)的解析式;
(2)求該函數(shù)的單調(diào)增區(qū)間;
(3)該函數(shù)的圖象可由![]() 的圖象經(jīng)過怎樣的平移和伸縮變換得到的?
的圖象經(jīng)過怎樣的平移和伸縮變換得到的?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列四個命題:
①若樣本數(shù)據(jù)![]() 的方差為
的方差為![]() ,則數(shù)據(jù)
,則數(shù)據(jù)![]() 的方差為
的方差為![]() ;
;
②“平面向量![]() 的夾角為銳角,則
的夾角為銳角,則![]() ”的逆命題為真命題;
”的逆命題為真命題;
③命題“![]() ,均有
,均有![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”;
”;
④![]() 是直線
是直線![]() 與直線
與直線![]() 平行的必要不充分條件.
平行的必要不充分條件.
其中正確的命題個數(shù)是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年為我國改革開放40周年,某事業(yè)單位共有職工600人,其年齡與人數(shù)分布表如下:
年齡段 |
|
|
|
|
人數(shù)(單位:人) | 180 | 180 | 160 | 80 |
約定:此單位45歲~59歲為中年人,其余為青年人,現(xiàn)按照分層抽樣抽取30人作為全市慶祝晚會的觀眾.
(1)抽出的青年觀眾與中年觀眾分別為多少人?
(2)若所抽取出的青年觀眾與中年觀眾中分別有12人和5人不熱衷關(guān)心民生大事,其余人熱衷關(guān)心民生大事.完成下列![]() 列聯(lián)表,并回答能否有
列聯(lián)表,并回答能否有![]() 的把握認為年齡層與熱衷關(guān)心民生大事有關(guān)?
的把握認為年齡層與熱衷關(guān)心民生大事有關(guān)?
熱衷關(guān)心民生大事 | 不熱衷關(guān)心民生大事 | 總計 | |
青年 | 12 | ||
中年 | 5 | ||
總計 | 30 |
(3)若從熱衷關(guān)心民生大事的青年觀眾(其中1人擅長歌舞,3人擅長樂器)中,隨機抽取2人上表演節(jié)目,則抽出的2人能勝任才藝表演的概率是多少?
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知首項均為![]() 的數(shù)列
的數(shù)列![]() ,
,![]() ,滿足
,滿足![]() .
.
(1)令![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式;
的通項公式;
(2)若數(shù)列![]() 為各項均為正數(shù)的等比數(shù)列,且
為各項均為正數(shù)的等比數(shù)列,且![]() ,設(shè)
,設(shè)![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com