Question

函數f（x）=x³+ax²+bx的圖象與x軸相切于點（-3，0），且函數存在極值．
（I）求函數f（x）的解析式及單調區間；
（II）過函數y=f（x）圖象上一點P₁（x₁，y₁）（P₁不是y=f（x）圖象的對稱中心）作曲線的切線，切于不同于P₁（x₁，y₁）的另一點P₂（x₂，y₂），再過P₂（x₂，y₂）作曲線的切線切于不同于P₂（x₂，y₂）的另一點P₃（x₃，y₃），…，過P_n（x_n，y_n）作曲線的切線切于不同于P_n（x_n，y_n）的另一點P_n+1（x_n+1，y_n+1），求x_n與x_n+1的關系．

Answer 1

分析：（I）對函數求導可得 f′（x）=3x²+2ax+b，由題意可得f（-3）=0，f′（-3）=0，代入可求a，b的值，然后根據導數的符號判斷函數的單調區間及極值
（II）可先設切點為（x_n+1，y_n+1），根據導數的幾何意義可得切線方程為y-y_n+1=f′（x_n+1）（x-x_n+1）=（3x_n+1²+12x_n+1+9）（x-x_n+1），又切線過點（x_n，y_n），所以代入切線方程整理求

解答：解：（I）f′（x）=3x²+2ax+b
由題意可得f（-3）=0，f′（-3）=0
∴

-27+9a-3b=0 27-6a+b=0

∴a=6，b=9

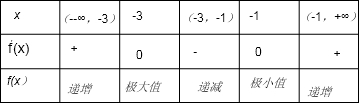
所以f（x）在（-∞，-3），（0，+∞）單調增區間
y_極大值=0y_極小值=-4
（II）設切點為（x_n+1，y_n+1）
∴切線方程為y-y_n+1=f′（x_n+1）（x-x_n+1）=（3x_n+1²+12x_n+1+9）（x-x_n+1）
又切線過點（x_n，y_n），所以代入切線方程整理可得：（x_n+2x_n+1）（x-x_n+1）+6（x_n-x_n+1）=0
∵x_n≠n_n+1∴x_n+2x_n+1+6=0

點評：利用導數的符號變化求解函數的單調區間及函數的極值是函數在導數部分最基本的考查，而切線方程的求解關鍵是要熟練應用導數的幾何意義．