
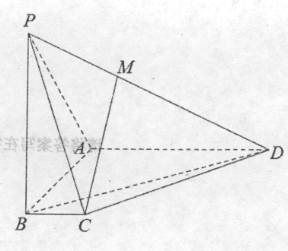
【題目】如圖,在四棱錐![]() 中:
中:![]() 底面ABCD,底面ABCD為梯形,
底面ABCD,底面ABCD為梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M為棱PD上的點。
,BC=1,M為棱PD上的點。
(Ⅰ)若![]() ,求證:
,求證:![]() 平面PAB;
平面PAB;
(Ⅱ)求直線BD與平面PAD所成角的大小;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)見解析(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)過點M作MH∥AD,交PA于H,連接BH,證明MH∥BC,CM∥BH,然后證明MC∥平面PAD.(Ⅱ)說明BC⊥AB.PB⊥AB,PB⊥BC,以B為原點,BC,BA,BP所在直線為x,y,z軸建立空間直角坐標系,求平面PAD的一個法向量,則可求出直線BD與平面PAD所成角(Ⅲ)求平面PCD的一個法向量,通過向量的數量積求解二面角![]() 的大小.
的大小.
(Ⅰ)過點M作MH∥AD,交PA于H,連接BH,
∵PM![]() PD,∴ HM
PD,∴ HM![]() AD=BC.
AD=BC.
又MH∥AD,AD∥BC,∴HM∥BC.
∴BCMH為平行四邊形,∴CM∥BH.
又BH平面PAB,CM平面PAB,
∴MC∥平面PAB.
(Ⅱ)∵梯形ABCD中,AD∥BC,AD⊥AB,∴BC⊥AB.
∵PB⊥平面ABCD,∴PB⊥AB,PB⊥BC,
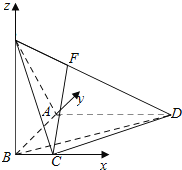
如圖,以B為原點,BC,BA,BP所在直線為x,y,z軸建立空間直角坐標系,
∴C(1,0,0),D(3,3,0),A(0,3,0),P(0,0,3).
設平面PAD的一個法向量為![]() (x,y,z),
(x,y,z),
∵![]() (3,3,﹣3),
(3,3,﹣3),![]() (3,0,0)
(3,0,0)
∴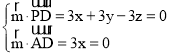 ,
,
取y=1得到![]() (0, 1,1),
(0, 1,1),
設直線BD與平面PAD所成角為![]() ,
,
∴sin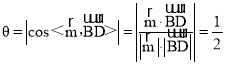 ,
,
∴直線BD與平面PAD所成角的大小為![]() .
.
(Ⅲ)設平面PCD的一個法向量為![]()
![]()
∴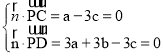 取c=1,得到
取c=1,得到![]()
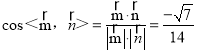 ,
,
∴二面角![]() 的余弦值為
的余弦值為![]()


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:
【題目】為了檢驗學習情況,某培訓機構于近期舉辦一場競賽活動,分別從甲、乙兩班各抽取10名學員的成績進行統計分析,其成績的莖葉圖如圖所示(單位:分),假設成績不低于90分者命名為“優秀學員”.
(1)分別求甲、乙兩班學員成績的平均分(結果保留一位小數);
(2)從甲班4名優秀學員中抽取兩人,從乙班2名80分以下的學員中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位后得到函數
個單位后得到函數![]() 的圖像,且函數
的圖像,且函數![]() 滿足
滿足![]() ,則下列命題中正確的是()
,則下列命題中正確的是()
A. 函數![]() 圖像的兩條相鄰對稱軸之間的距離為
圖像的兩條相鄰對稱軸之間的距離為![]()
B. 函數![]() 圖像關于點
圖像關于點![]() 對稱
對稱
C. 函數![]() 圖像關于直線
圖像關于直線![]() 對稱
對稱
D. 函數![]() 在區間
在區間![]() 內為單調遞減函數
內為單調遞減函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三家企業產品的成本分別為10000,12000,15000,其成本構成如下圖所示,則關于這三家企業下列說法錯誤的是( )
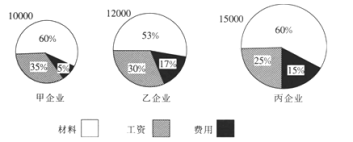
A.成本最大的企業是丙企業B.費用支出最高的企業是丙企業
C.支付工資最少的企業是乙企業D.材料成本最高的企業是丙企業
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 過點
過點![]() ,且離心率為
,且離心率為![]()
(Ⅰ)求橢圓C的方程;
(Ⅱ)若過原點的直線![]() 與橢圓C交于P、Q兩點,且在直線
與橢圓C交于P、Q兩點,且在直線![]() 上存在點M,使得
上存在點M,使得![]() 為等邊三角形,求直線
為等邊三角形,求直線![]() 的方程。
的方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com