Question

【題目】已知中心在坐標原點，焦點在軸上的橢圓過點，且它的離心率

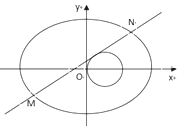
（I）求橢圓的標準方程；

（II）與圓相切的直線交橢圓于、兩點，若橢圓上一點滿足，求實數的取值范圍

Answer 1

【答案】（1）；（2）

【解析】

（1）根據題意先設出橢圓的標準方程，然后根據橢圓上的點及離心率可求出方程中的待定系數，進而可得所求的方程；（2）由直線和圓相切可得(t≠0)，然后將直線方程代入橢圓方程后得到關于x的一元二次方程，根據根據系數的關系可得點C的坐標，代入橢圓方程后整理得到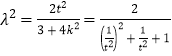，根據的范圍可得，進而得到所求范圍．

（1）設橢圓的標準方程為，

由已知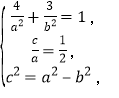得解得

所以橢圓的標準方程為.

（2）因為直線：y＝kx＋t與圓(x－1)2＋y2＝1相切，

所以＝1，

整理得(t≠0)．

由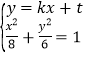消去y整理得(3＋4k2)x2＋8ktx＋4t2－24＝0，

因為直線與橢圓交于M，N兩點，

所以，

將代入上式可得恒成立．

設M(x1，y1)，N(x2，y2)，

則有x1＋x2＝－，

所以y1＋y2＝kx1＋t＋kx2＋t＝k(x1＋x2)＋2t＝，

因為 )，

所以可得C，

又因為點C在橢圓上，

所以＋＝1,

所以，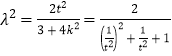

因為t2＞0，所以＋＋1＞1，

所以，

所以的取值范圍為.