【題目】拿破侖為人好學，是法蘭西科學院院士，他對數學方面很感興趣，在行軍打仗的空閑時間，經常研究平面幾何。他提出了著名的拿破侖定理：以三角形各邊為邊分別向外（內）側作等邊三角形，則它們的中心構成一個等邊三角形。如圖所示，以等邊
的三條邊為邊，向外作
個正三角形，取它們的中心
，順次連接，得到
，圖中陰影部分為與的公共部分。若往
中投擲一點，則該點落在陰影部分內的概率為（ ）
A. 
B. 
C. 
D. 
舉一反三同步巧講精練系列答案
口算與應用題卡系列答案科目：高中數學 來源： 題型：
【題目】現行的個稅法修正案規定：個稅免征額由原來的2000元提高到3500元，并給出了新的個人所得稅稅率表：
全月應納稅所得額 | 稅率 |
不超過1500元的部分 | 3% |
超過1500元至4500元的部分 | 10% |
超過4500元至9000元的部分 | 20% |
超過9000元至35000元的部分 | 25% |
…… | … |
例如某人的月工資收入為5000元，那么他應納個人所得稅為：
（元）.
（Ⅰ）若甲的月工資收入為6000元，求甲應納的個人收的稅；
（Ⅱ）設乙的月工資收入為
元，應納個人所得稅為
元，求關于
的函數；
（Ⅲ）若丙某月應納的個人所得稅為1000元，給出丙的月工資收入.（結論不要求證明）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
是圓
上的任意一點，
是過點且與
軸垂直的直線，
是直線與軸的交點，點
在直線上，且滿足
.當點在圓
上運動時，記點的軌跡為曲線
.
（1）求曲線的方程；
（2）已知直線
與曲線交于
，
兩點，點關于
軸的對稱點為
，證明：直線
過定點
.
查看答案和解析>>
科目：高中數學 來源： 題型：
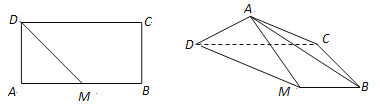
【題目】如圖，在矩形ABCD中，AB＝2，AD＝1，M為AB的中點，將△ADM沿DM翻折．在翻折過程中，當二面角A—BC—D的平面角最大時，其正切值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
是一個
的方格表，在每一個小方格內各填一個正整數.若中的一個
方格表的所有數的和為10的倍數，則稱其為“好矩形”；若中的一個
的小方格不包含于任何一個好矩形，則稱其為“壞格”.求中壞格個數的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】水果的價格會受到需求量和天氣的影響.某采購員定期向某批發商購進某種水果，每箱水果的價格會在當日市場價的基礎上進行優惠，購買量越大優惠幅度越大，采購員通過對以往的10組數據進行研究，發現可采用
來作為價格的優惠部分
（單位：元/箱）與購買量
（單位：箱）之間的回歸方程，整理相關數據得到下表（表中
）：
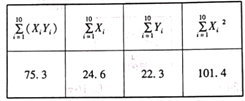
（1）根據參考數據，
①建立關于的回歸方程；
②若當日該種水果的市場價為200元/箱，估算購買100箱該種水果所需的金額（精確到0.1元）.
（2）在樣本中任取一點，若它在回歸曲線上或上方，則稱該點為高效點.已知這10個樣本點中，高效點有4個，現從這10個點中任取3個點，設取到高效點的個數為
，求的數學期望.
附：對于一組數據
，
，…，
，其回歸直線
的斜率和截距的最小二乘估計分別為
，
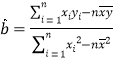，參考數據：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是平面內凸三十五邊形的35個頂點，且中任何兩點之間的距離不小于
. 證明：從這35個點中可以選出五個點，使得這五個點中任意兩點之間的距離不小于3．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一布袋中裝有
個小球，甲，乙兩個同學輪流且不放回的抓球，每次最少抓一個球，最多抓三個球，規定：由乙先抓，且誰抓到最后一個球誰贏，那么以下推斷中正確的是（ ）
A. 若
，則乙有必贏的策略B. 若
，則甲有必贏的策略
C. 若
，則甲有必贏的策略D. 若
，則乙有必贏的策略
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
