
【題目】試求正數![]() 的最大值,使得點集
的最大值,使得點集![]() 一定被包含于另一個點集
一定被包含于另一個點集![]() ,且對任何
,且對任何![]() ,都有
,都有![]() 之中.
之中.
【答案】![]()
【解析】
![]() 集即為由直線
集即為由直線![]() 確定的上半平面的交集(
確定的上半平面的交集(![]() 不同,相對應的上半平面一般也不同,但所有的這種上半平面有公共部分即交集;另外,可以規定上半平面也包含了這條直線).而半徑為
不同,相對應的上半平面一般也不同,但所有的這種上半平面有公共部分即交集;另外,可以規定上半平面也包含了這條直線).而半徑為![]() 的圓的圓心
的圓的圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.
由題意知,![]() 應滿足
應滿足![]() .故
.故![]() 的最大值是
的最大值是![]() 的最小值.
的最小值.
而![]()
![]() ,
,
等號成立當且僅當![]() ,即
,即![]() 時成立.
時成立.
故![]() .
.
另解:把![]() 等價地改寫為
等價地改寫為![]() .
.
令![]() ,則
,則![]() .
.
下而分兩種情形討論![]() 的情況:
的情況:
(1)若對稱軸![]() 或
或![]() 即
即![]() 或
或![]() )時,
)時,
只須當![]() 時有
時有![]() ,
,
即![]() (
(![]() 或
或![]() ). ①
). ①
(2)若對稱軸![]() ,即
,即![]() 時,只須判別式
時,只須判別式![]() ,
,
即![]() . ②
. ②
以上的①和②刻畫了集![]() ①和②}.
①和②}.
設圓![]() 與拋物線
與拋物線![]() 相切,消去
相切,消去![]() 得
得![]() ,即
,即![]() .
.
令其判別式![]() 得
得![]() ,解得
,解得![]() .
.
此時![]() ,
,![]() .
.
而點![]() 到直線
到直線![]() 的距離為
的距離為![]() (如圖),
(如圖),
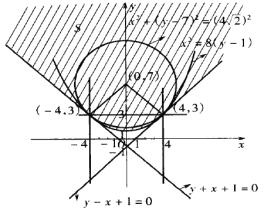
故由上述結果可知![]() .(
.(![]() 不能再大,否則越出
不能再大,否則越出![]() 的區域).
的區域).
注:區域![]() 是圖中的陰影部分.
是圖中的陰影部分.


科目:高中數學 來源: 題型:
【題目】為慶祝黨的98歲生日,某高校組織了“歌頌祖國,緊跟黨走”為主題的黨史知識競賽。從參加競賽的學生中,隨機抽取40名學生,將其成績分為六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如圖所示的頻率分布直方圖.
,到如圖所示的頻率分布直方圖.

(1)求圖中![]() 的值及樣本的中位數與眾數;
的值及樣本的中位數與眾數;
(2)若從競賽成績在![]() 與
與![]() 兩個分數段的學生中隨機選取兩名學生,設這兩名學生的競賽成績之差的絕對值不大于
兩個分數段的學生中隨機選取兩名學生,設這兩名學生的競賽成績之差的絕對值不大于![]() 分為事件
分為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
(3)為了激勵同學們的學習熱情,現評出一二三等獎,得分在![]() 內的為一等獎,得分在
內的為一等獎,得分在![]() 內的為二等獎, 得分在
內的為二等獎, 得分在![]() 內的為三等獎.若將頻率視為概率,現從考生中隨機抽取三名,設
內的為三等獎.若將頻率視為概率,現從考生中隨機抽取三名,設![]() 為獲得三等獎的人數,求
為獲得三等獎的人數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,A為C上異于原點的任意一點,以點F為圓心且過點A的圓M與x軸正半軸交于點B,AB的延長線交C于點D,AF的延長線交C于點E.
的焦點為F,A為C上異于原點的任意一點,以點F為圓心且過點A的圓M與x軸正半軸交于點B,AB的延長線交C于點D,AF的延長線交C于點E.

(1)若點A的縱坐標為4,求圓M的方程;
(2)若線段AD的中點為G,求證:![]() 軸;
軸;
(3)![]() 的面積是否存在最小值?若存在,請求出此最小值;若不存在,請說明理由.
的面積是否存在最小值?若存在,請求出此最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知兩個變量線性相關,若它們的相關性越強,則相關系數的絕對值越接近于1.
(2)線性回歸直線必過點![]() ;
;
(3)對于分類變量A與B的隨機變量![]() ,
,![]() 越大說明“A與B有關系”的可信度越大.
越大說明“A與B有關系”的可信度越大.
(4)在刻畫回歸模型的擬合效果時,殘差平方和越小,相關指數![]() 的值越大,說明擬合的效果越好.
的值越大,說明擬合的效果越好.
(5)根據最小二乘法由一組樣本點![]() ,求得的回歸方程是
,求得的回歸方程是![]() ,對所有的解釋變量
,對所有的解釋變量![]() ,
,![]() 的值一定與
的值一定與![]() 有誤差.
有誤差.
以上命題正確的序號為____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.且曲線
軸的正半軸為極軸建立極坐標系.且曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程以及曲線
的普通方程以及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有2002名運動員,號碼依次為![]() .從中選出若干名運動員參加儀仗隊,但要使剩下的運動員中沒有一個人的號碼數等于另外兩人的號碼數的乘積.那么,被選為儀仗隊的運動員至少能有多少人?給出你的選取方案,并簡述理由.
.從中選出若干名運動員參加儀仗隊,但要使剩下的運動員中沒有一個人的號碼數等于另外兩人的號碼數的乘積.那么,被選為儀仗隊的運動員至少能有多少人?給出你的選取方案,并簡述理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秉持“綠水青山就是金山銀山”的生態文明發展理念,為推動新能源汽車產業迅速發展,有必要調查研究新能源汽車市場的生產與銷售.下圖是我國某地區![]() 年至
年至![]() 年新能源汽車的銷量(單位:萬臺)按季度(一年四個季度)統計制成的頻率分布直方圖.
年新能源汽車的銷量(單位:萬臺)按季度(一年四個季度)統計制成的頻率分布直方圖.
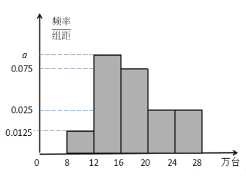
(1)求直方圖中![]() 的值,并估計銷量的中位數;
的值,并估計銷量的中位數;
(2)請根據頻率分布直方圖估計新能源汽車平均每個季度的銷售量(同一組數據用該組中間值代表),并以此預計![]() 年的銷售量.
年的銷售量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某直三棱柱被削去上底后所得幾何體的左視圖、俯視圖、直觀圖,在直觀圖中,M是BD的中點,左視圖是直角梯形,俯視圖是等腰直角三角形,有關數據如圖所示.
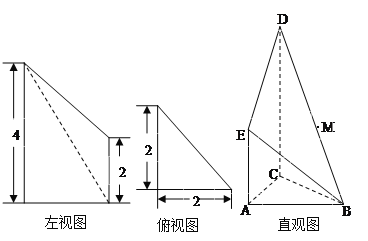
(Ⅰ)求該幾何體的表面積和體積;
(Ⅱ)求點C到平面MAB的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店剛剛上市了《中國古代數學史》,銷售前該書店擬定了5種單價進行試銷,每種單價(![]() 元)試銷l天,得到如表單價
元)試銷l天,得到如表單價![]() (元)與銷量
(元)與銷量![]() (冊)數據:
(冊)數據:
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
(l)根據表中數據,請建立![]() 關于
關于![]() 的回歸直線方程:
的回歸直線方程:
(2)預計今后的銷售中,銷量![]() (冊)與單價
(冊)與單價![]() (元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
(元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com