
【題目】已知函數(shù)![]() .
.
(1)判斷并證明函數(shù)![]() 的奇偶性;
的奇偶性;
(2)判斷當(dāng)![]() 時函數(shù)
時函數(shù)![]() 的單調(diào)性,并用定義證明;
的單調(diào)性,并用定義證明;
(3)若![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]() ,解不等式
,解不等式![]() .
.
【答案】(1)奇函數(shù)(2)增函數(shù)(3)![]()
【解析】試題分析:(1)判斷與證明函數(shù)的奇偶性,首先要確定函數(shù)的定義域是否關(guān)于原點(diǎn)對稱,再判斷f(-x)與f(x)的關(guān)系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數(shù),如果f(-x)=-f(x)就是奇函數(shù),否則是非奇非偶函數(shù)。(2)利函數(shù)單調(diào)性定義證明單調(diào)性,按假設(shè),作差,化簡,判斷,下結(jié)論五個步驟。(3)由(1)(2)奇函數(shù)![]() 在(-1,1)為單調(diào)函數(shù),
在(-1,1)為單調(diào)函數(shù),
原不等式變形為f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函數(shù)的單調(diào)性及定義(-1,1)求解得x范圍。
試題解析:(1)函數(shù)![]() 為奇函數(shù).證明如下:
為奇函數(shù).證明如下:
![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]()
又![]()
![]() 為奇函數(shù)
為奇函數(shù)
(2)函數(shù)![]() 在(-1,1)為單調(diào)函數(shù).證明如下:
在(-1,1)為單調(diào)函數(shù).證明如下:
任取![]() ,則
,則


![]()
![]() ,
, ![]()

即![]()
故![]() 在(-1,1)上為增函數(shù)
在(-1,1)上為增函數(shù)
(3)由(1)、(2)可得
![]() 則
則
 解得:
解得: ![]()
所以,原不等式的解集為![]()
【點(diǎn)睛】
(1)奇偶性:判斷與證明函數(shù)的奇偶性,首先要確定函數(shù)的定義域是否關(guān)于原點(diǎn)對稱,再判斷f(-x)與f(x)的關(guān)系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數(shù),如果f(-x)=-f(x)就是奇函數(shù),否則是非奇非偶函數(shù)。
(2)單調(diào)性:利函數(shù)單調(diào)性定義證明單調(diào)性,按假設(shè),作差,化簡,定號,下結(jié)論五個步驟。
【題型】解答題
【結(jié)束】
22
【題目】已知函數(shù)![]() .
.
(1)若![]() 的定義域和值域均是
的定義域和值域均是![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),且對任意的
上是減函數(shù),且對任意的![]() ,都有
,都有![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,且對任意的
,且對任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:(1)先利用二次函數(shù)的性質(zhì)確定函數(shù)![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,故
,故![]() 在
在![]() 單調(diào)遞減,然后由定義域與值域列出等式關(guān)系,從而求解即可;(2)由(1)可知
單調(diào)遞減,然后由定義域與值域列出等式關(guān)系,從而求解即可;(2)由(1)可知![]() ,初步確定
,初步確定![]() 的取值范圍
的取值范圍![]() ,然后確定
,然后確定![]() 時函數(shù)
時函數(shù)![]() 的最大值
的最大值![]() ,從中求解不等式組
,從中求解不等式組![]() 即可;(3)將“對任意的
即可;(3)將“對任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立”轉(zhuǎn)化為
成立”轉(zhuǎn)化為![]() 時,
時,![]() 的值域包含了
的值域包含了![]() 在
在![]() 的值域,然后進(jìn)行分別求
的值域,然后進(jìn)行分別求![]() 在
在![]() 的值域,從集合間的包含關(guān)系即可求出
的值域,從集合間的包含關(guān)系即可求出![]() 的取值范圍.
的取值范圍.
試題解析:(1)∵![]()
∴![]() 在
在![]() 上單調(diào)遞減,又
上單調(diào)遞減,又![]() ,∴
,∴![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 4分
4分
(2)∵![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),∴
上是減函數(shù),∴![]() ,∴
,∴![]()
∴![]() ,
,![]()
∴![]() 時,
時,![]()
又∵對任意的![]() ,都有
,都有![]() ,
,
∴![]() ,即
,即![]() ,也就是
,也就是![]()
綜上可知![]() 8分
8分
(3)∵![]() 在
在![]() 上遞增,
上遞增,![]() 在
在![]() 上遞減,
上遞減,
當(dāng)![]() 時,
時,![]() ,
,![]()
∵對任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立
成立
∴![]()
![]()
∴![]() ,所以
,所以![]() 13分
13分


 贏在課堂名師課時計(jì)劃系列答案
贏在課堂名師課時計(jì)劃系列答案 天天向上課時同步訓(xùn)練系列答案
天天向上課時同步訓(xùn)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l:x-2y+2m-2=0.
(1)求過點(diǎn)(2,3)且與直線l垂直的直線的方程;
(2)若直線l與兩坐標(biāo)軸所圍成的三角形的面積大于4,求實(shí)數(shù)m的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)由直線![]() 的斜率為
的斜率為![]() ,可得所求直線的斜率為
,可得所求直線的斜率為![]() ,代入點(diǎn)斜式方程,可得答案;(2)直線
,代入點(diǎn)斜式方程,可得答案;(2)直線![]() 與兩坐標(biāo)軸的交點(diǎn)分別為
與兩坐標(biāo)軸的交點(diǎn)分別為![]() ,則所圍成的三角形的面積為
,則所圍成的三角形的面積為![]() ,根據(jù)直線
,根據(jù)直線![]() 與兩坐標(biāo)軸所圍成的三角形的面積為大于
與兩坐標(biāo)軸所圍成的三角形的面積為大于![]() ,構(gòu)造不等式,解得答案.
,構(gòu)造不等式,解得答案.
試題解析:(1)與直線l垂直的直線的斜率為-2,
因?yàn)辄c(diǎn)(2,3)在該直線上,所以所求直線方程為y-3=-2(x-2),
故所求的直線方程為2x+y-7=0.
(2) 直線l與兩坐標(biāo)軸的交點(diǎn)分別為(-2m+2,0),(0,m-1),
則所圍成的三角形的面積為![]() ×|-2m+2|×|m-1|.
×|-2m+2|×|m-1|.
由題意可知![]() ×|-2m+2|×|m-1|>4,化簡得(m-1)2>4,
×|-2m+2|×|m-1|>4,化簡得(m-1)2>4,
解得m>3或m<-1,
所以實(shí)數(shù)m的取值范圍是(-∞,-1)∪(3,+∞).
【方法點(diǎn)睛】本題主要考查直線的方程,兩條直線平行與斜率的關(guān)系,屬于簡單題. 對直線位置關(guān)系的考查是熱點(diǎn)命題方向之一,這類問題以簡單題為主,主要考查兩直線垂直與兩直線平行兩種特殊關(guān)系:在斜率存在的前提下,(1)![]() ;(2)
;(2)![]() ,這類問題盡管簡單卻容易出錯,特別是容易遺忘斜率不存在的情況,這一點(diǎn)一定不能掉以輕心.
,這類問題盡管簡單卻容易出錯,特別是容易遺忘斜率不存在的情況,這一點(diǎn)一定不能掉以輕心.
【題型】解答題
【結(jié)束】
18
【題目】在平面直角坐標(biāo)系![]() 中,已知經(jīng)過原點(diǎn)O的直線
中,已知經(jīng)過原點(diǎn)O的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(diǎn)。
兩點(diǎn)。
(1)若直線![]() 與圓
與圓![]() 相切,切點(diǎn)為B,求直線
相切,切點(diǎn)為B,求直線![]() 的方程;
的方程;
(2)若![]() ,求直線
,求直線![]() 的方程;
的方程;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】口袋中裝有2個白球和n(n≥2,n ![]() N*)個紅球.每次從袋中摸出2個球(每次摸球后把這2個球放回口袋中),若摸出的2個球顏色相同則為中獎,否則為不中獎.
N*)個紅球.每次從袋中摸出2個球(每次摸球后把這2個球放回口袋中),若摸出的2個球顏色相同則為中獎,否則為不中獎.
(I)用含n的代數(shù)式表示1次摸球中獎的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中獎的概率;
(III)記3次摸球中恰有1次中獎的概率為f(p),當(dāng)f(p)取得最大值時,求n的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將函數(shù)y=cos2x的圖象向左平移 ![]() 個單位,得到函數(shù)y=f(x)cosx的圖象,則f(x)的表達(dá)式可以是( )
個單位,得到函數(shù)y=f(x)cosx的圖象,則f(x)的表達(dá)式可以是( )
A.f(x)=﹣2sinx
B.f(x)=2sinx
C.f(x)= ![]() sin2x
sin2x
D.f(x)= ![]() (sin2x+cos2x)
(sin2x+cos2x)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 的最小值為3,且
的最小值為3,且![]() .
.
求函數(shù)![]() 的解析式;
的解析式;
(2)若偶函數(shù)![]() (其中
(其中![]() ),那么,
),那么, ![]() 在區(qū)間
在區(qū)間![]() 上是否存在零點(diǎn)?請說明理由.
上是否存在零點(diǎn)?請說明理由.
【答案】(1)![]() (2)存在零點(diǎn)
(2)存在零點(diǎn)
【解析】試題分析:(1)待定系數(shù)法,己知函數(shù)類型為二次函數(shù),又知f(-1)=f(3),所以對稱軸是x=1,且函數(shù)最小值f(1)=3,所設(shè)函數(shù)![]() ,且
,且![]() ,代入f(-1)=11,可解a。
,代入f(-1)=11,可解a。
(2)由題意可得![]() ,代入
,代入![]() ,由
,由![]() 和根的存在性定理,
和根的存在性定理, ![]() 在區(qū)間(1,2)上存在零點(diǎn)。
在區(qū)間(1,2)上存在零點(diǎn)。
試題解析:(1)因?yàn)?/span>![]() 是二次函數(shù),且
是二次函數(shù),且![]()
所以二次函數(shù)圖像的對稱軸為![]() .
.
又![]() 的最小值為3,所以可設(shè)
的最小值為3,所以可設(shè)![]() ,且
,且![]()
由![]() ,得
,得![]()
所以![]()
(2)由(1)可得![]() ,
,
因?yàn)?/span>![]() ,
,
![]()
所以![]() 在區(qū)間(1,2)上存在零點(diǎn).
在區(qū)間(1,2)上存在零點(diǎn).
【點(diǎn)睛】
(1)對于求己知類型函數(shù)的的解析式,常用待定系數(shù)法,由于二次函數(shù)的表達(dá)式形式比較多,有一般式,兩點(diǎn)式,頂點(diǎn)式,由本題所給條件知道對稱軸與頂點(diǎn)坐標(biāo),所以設(shè)頂點(diǎn)式。
(2)對于判定函數(shù)在否存在零點(diǎn)問題,一般解決此類問題的三步曲是:①先通過觀察函數(shù)圖象再估算出根所在的區(qū)間;②根據(jù)方程根的存在性定理證明根是存在的;③最后根據(jù)函數(shù)的性質(zhì)證明根是唯一的.本題給了區(qū)間,可直接用根的存在性定理。
【題型】解答題
【結(jié)束】
20
【題目】《中華人民共和國個人所得稅》規(guī)定,公民月工資、薪金所得不超過3500元的部分不納稅,超過3500元的部分為全月稅所得額,此項(xiàng)稅款按下表分段累計(jì)計(jì)算:
全月應(yīng)納稅所得額 | 稅率 |
不超過1500元的部分 |
|
超過1500元至4500元的部分 |
|
超過4500元至9000元的部分 |
|
(1)已知張先生的月工資,薪金所得為10000元,問他當(dāng)月應(yīng)繳納多少個人所得稅?
(2)設(shè)王先生的月工資,薪金所得為![]() ,當(dāng)月應(yīng)繳納個人所得稅為
,當(dāng)月應(yīng)繳納個人所得稅為![]() 元,寫出
元,寫出![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)已知王先生一月份應(yīng)繳納個人所得稅為303元,那么他當(dāng)月的工資、薪金所得為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)判斷并證明函數(shù)![]() 的奇偶性;
的奇偶性;
(2)判斷當(dāng)![]() 時函數(shù)
時函數(shù)![]() 的單調(diào)性,并用定義證明;
的單調(diào)性,并用定義證明;
(3)若![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]() ,解不等式
,解不等式![]() .
.
【答案】(1)奇函數(shù)(2)增函數(shù)(3)![]()
【解析】試題分析:(1)判斷與證明函數(shù)的奇偶性,首先要確定函數(shù)的定義域是否關(guān)于原點(diǎn)對稱,再判斷f(-x)與f(x)的關(guān)系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數(shù),如果f(-x)=-f(x)就是奇函數(shù),否則是非奇非偶函數(shù)。(2)利函數(shù)單調(diào)性定義證明單調(diào)性,按假設(shè),作差,化簡,判斷,下結(jié)論五個步驟。(3)由(1)(2)奇函數(shù)![]() 在(-1,1)為單調(diào)函數(shù),
在(-1,1)為單調(diào)函數(shù),
原不等式變形為f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函數(shù)的單調(diào)性及定義(-1,1)求解得x范圍。
試題解析:(1)函數(shù)![]() 為奇函數(shù).證明如下:
為奇函數(shù).證明如下:
![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]()
又![]()
![]() 為奇函數(shù)
為奇函數(shù)
(2)函數(shù)![]() 在(-1,1)為單調(diào)函數(shù).證明如下:
在(-1,1)為單調(diào)函數(shù).證明如下:
任取![]() ,則
,則
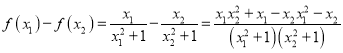
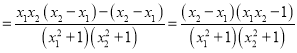
![]()
![]() ,
, ![]()
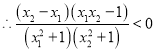
即![]()
故![]() 在(-1,1)上為增函數(shù)
在(-1,1)上為增函數(shù)
(3)由(1)、(2)可得
![]() 則
則
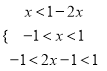 解得:
解得: ![]()
所以,原不等式的解集為![]()
【點(diǎn)睛】
(1)奇偶性:判斷與證明函數(shù)的奇偶性,首先要確定函數(shù)的定義域是否關(guān)于原點(diǎn)對稱,再判斷f(-x)與f(x)的關(guān)系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數(shù),如果f(-x)=-f(x)就是奇函數(shù),否則是非奇非偶函數(shù)。
(2)單調(diào)性:利函數(shù)單調(diào)性定義證明單調(diào)性,按假設(shè),作差,化簡,定號,下結(jié)論五個步驟。
【題型】解答題
【結(jié)束】
22
【題目】已知函數(shù)![]() .
.
(1)若![]() 的定義域和值域均是
的定義域和值域均是![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),且對任意的
上是減函數(shù),且對任意的![]() ,都有
,都有![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,且對任意的
,且對任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知:函數(shù)![]()
![]() 求函數(shù)
求函數(shù)![]() 的周期T與單調(diào)增區(qū)間.
的周期T與單調(diào)增區(qū)間.
![]() 函數(shù)
函數(shù)![]() 與
與![]() 的圖象有幾個公共交點(diǎn).
的圖象有幾個公共交點(diǎn).
![]() 設(shè)關(guān)于x的函數(shù)
設(shè)關(guān)于x的函數(shù)![]() 的最小值為
的最小值為![]() ,試確定滿足
,試確定滿足![]() 的a的值.
的a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】王先生家住 A 小區(qū),他工作在 B 科技園區(qū),從家開車到公司上班路上有 L1 , L2 兩條路線(如圖),L1 路線上有 A1 , A2 , A3 三個路口,各路口遇到紅燈的概率均為 ![]() ;L2 路線上有 B1 , B2 兩個路.各路口遇到紅燈的概率依次為
;L2 路線上有 B1 , B2 兩個路.各路口遇到紅燈的概率依次為 ![]() ,
, ![]() .若走 L1 路線,王先生最多遇到 1 次紅燈的概率為;若走 L2 路線,王先生遇到紅燈次數(shù) X 的數(shù)學(xué)期望為 .
.若走 L1 路線,王先生最多遇到 1 次紅燈的概率為;若走 L2 路線,王先生遇到紅燈次數(shù) X 的數(shù)學(xué)期望為 . 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知A,B,C為直角坐標(biāo)系xOy中的三個定點(diǎn)
(Ⅰ)若點(diǎn)D為□ABCD的第四個頂點(diǎn),求|![]() |;
|;
(Ⅱ)若點(diǎn)P在直線OC上,且![]() ·
·![]() =4,求點(diǎn)P的坐標(biāo).
=4,求點(diǎn)P的坐標(biāo).

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com