【題目】已知函數
（
），
，
．
（1）求函數
的單調區間；
（2）當
時，
的兩個極值點為
，
（
）．
①證明：
；
②若
，
恰為
的零點，求
的最小值．
【答案】(1)當
時，
的單調增區間為
，單調減區間為
，當
時，
的單調遞增區間為
；(2)①證明見解析；②
．
【解析】
試題分析：(1)對函數求導，對參數
分類討論，利用導數的正負求得函數的單調區間；(2)①對函數求導得
，得
的兩根
,
即為方程
的兩根；利用韋達定理得
，
，令
（
），由
，得
，兩邊同時除以
，得
，且
，求得
的取值范圍，從而證得結論；②由
，
為
的零點，代入相減得
，故
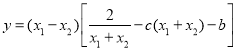
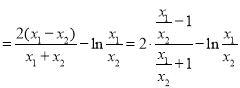，令
（
），
，求導后利用函數的單調性求得其最小值，從而求得所求結果.
試題解析：（1）∵函數
，∴
，
；
當
時，由
解得
，即當
時，
，
單調遞增；
由
解得
，即當
時，
，
單調遞減；
當
時，
，故
，即
在
上單調遞增；
∴當時，的單調增區間為，單調減區間為；
當時，的單調遞增區間為．
（2）①
，則，
∴的兩根,即為方程的兩根；
又∵
，∴
，，
令（），由，得，
因為
，兩邊同時除以，得，且，
故
，解得
或
，∴
，即
．
②∵，為的零點，
∴
，
，
兩式相減得，
∵
，
∴，
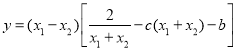
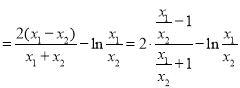令（），，
則
，
在
上是減函數，
∴
，
即
的最小值為．
計算高手系列答案科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝x3－3ax－1，a≠0.
(1)求f(x)的單調區間；
(2)若f(x)在x＝－1處取得極值，直線y＝m與y＝f(x)的圖象有三個不同的交點，求m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
.
（1）求函數
在
上的最小值；
（2）對一切
，
恒成立，求實數
的取值范圍；
（3）探討函數
是否存在零點？若存在，求出函數
的零點；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某水泥廠銷售工作人員根據以往該廠的銷售情況，繪制了該廠日銷售量的頻率分布直方圖，如圖所示：
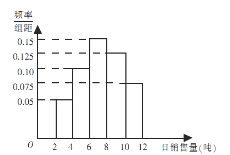
將日銷售量落入各組的頻率視為概率，并假設每天的銷售量相互獨立.
（1）求未來3天內，連續2天日銷售量不低于8噸，另一天日銷售量低于8噸的概率；
（2）用
表示未來3天內日銷售量不低于8噸的天數，求隨機變量
的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一盒中放有的黑球和白球，其中黑球4個，白球5個.
（1）從盒中同時摸出兩個球，求兩球顏色恰好相同的概率.
（2）從盒中摸出一個球，放回后再摸出一個球，求兩球顏色恰好不同的概率.
（3）從盒中不放回的每次摸一球，若取到白球則停止摸球，求取到第三次時停止摸球的概率
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】東亞運動會將于2013年10月6日在天津舉行．為了搞好接待工作，組委會打算學習北京奧運會招募大量志愿者的經驗，在某學院招募了16名男志愿者和14名女志愿者，調查發現，男女志愿者中分別有10人和6人喜愛運動，其余人不喜歡運動．
(1)根據以上數據完成以下2×2列聯表：
喜愛運動 | 不喜愛運動 | 總計 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
總計 | 30 |
(2)根據列聯表的獨立性檢驗，能否在犯錯誤的概率不超過0.10的前提下認為性別與喜愛運動有關？
(3)如果從喜歡運動的女志愿者中(其中恰有4人會外語)，抽取2名負責翻譯工作，那么抽出的志愿者中至少有1人能勝任翻譯工作的概率是多少？
參考公式：K2＝
，其中
n＝a＋b＋c＋d.
參考數據：
P(K2≥k) | 0.40 | 0.25 | 0.10 | 0.010 |
k | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
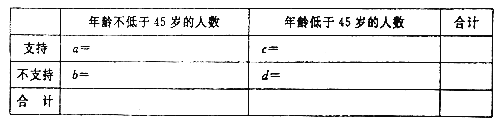
【題目】為了解人們對于國家新頒布的“生育二胎放開”政策的熱度，現在某市進行調查，隨機抽調了50人，他們年齡的頻數分布及支持“生育二胎”人數如下表：
（1）由以上統計數據填下面
列聯表，并問是否有99%的把握認為以45歲為分界點對“生育二胎放開”政策的支持度有差異；
（2）若對年齡在
的被調查人中各隨機選取兩人進行調查，恰好這兩人都支持“生育二胎放開”的概率是多少？
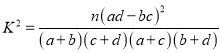
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
