
【題目】設函數![]() (
(![]() ),
),![]() ,
,
(Ⅰ) 試求曲線![]() 在點
在點![]() 處的切線l與曲線
處的切線l與曲線![]() 的公共點個數;(Ⅱ) 若函數
的公共點個數;(Ⅱ) 若函數![]() 有兩個極值點,求實數a的取值范圍.
有兩個極值點,求實數a的取值范圍.
(附:當![]() ,x趨近于0時,
,x趨近于0時, ![]() 趨向于
趨向于![]() )
)
【答案】(1)兩個公共點;(2)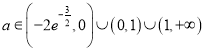 .
.
【解析】試題分析:(1)計算出![]() 及
及![]() ,根據點斜式可得切線方程,將切線方程與
,根據點斜式可得切線方程,將切線方程與![]() 聯立可得方程
聯立可得方程![]() ,設
,設![]() ,對其求導,可得其在
,對其求導,可得其在![]() 內的單調性,結合
內的單調性,結合![]() ,
, ![]() ,可得零點個數;(2)題意等價于
,可得零點個數;(2)題意等價于![]() 在
在![]() 至少有兩不同根,當
至少有兩不同根,當![]() 時,
時, ![]() 是
是![]() 的根,根據圖象的交點可知
的根,根據圖象的交點可知![]() 有一個零點,除去同根;當
有一個零點,除去同根;當![]() 顯然不合題意;當
顯然不合題意;當![]() 時,題意等價于
時,題意等價于![]() 在
在![]() 至少有兩不同根,對其求導判斷單調性,考慮極值與兩端的極限值可得結果.
至少有兩不同根,對其求導判斷單調性,考慮極值與兩端的極限值可得結果.
試題解析:(1)∵![]() ,
, ![]() ,
,
切線![]() 的斜率為
的斜率為![]() ,
,
∴切線![]() 的方程為
的方程為![]() ,即
,即![]() ,
,
聯立![]() ,得
,得![]() ;
;
設![]() ,則
,則![]() ,
,
由![]() 及
及![]() ,得
,得![]() 或
或![]() ,
,
∴![]() 在
在![]() 和
和![]() 上單調遞增,可知
上單調遞增,可知![]() 在
在![]() 上單調遞減,
上單調遞減,
又![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() ,
,
∴方程![]() 有兩個根:1和
有兩個根:1和![]() ,從而切線
,從而切線![]() 與曲線
與曲線![]() 有兩個公共點.
有兩個公共點.
(2)由題意知![]() 在
在![]() 至少有兩不同根,
至少有兩不同根,
設![]() ,
,
①當![]() 時,
時, ![]() 是
是![]() 的根,
的根,
由![]() 與
與![]() (
(![]() )恰有一個公共點,可知
)恰有一個公共點,可知![]() 恰有一根
恰有一根![]() ,
,
由![]() 得
得![]() ,不合題意,
,不合題意,
∴當![]() 且
且![]() 時,檢驗可知
時,檢驗可知![]() 和
和![]() 是
是![]() 的兩個極值點;
的兩個極值點;
②當![]() 時,
時, ![]() 在
在![]() 僅一根,所以
僅一根,所以![]() 不合題意;--9分
不合題意;--9分
③當![]() 時,需
時,需![]() 在
在![]() 至少有兩不同根,
至少有兩不同根,
由![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
可知![]() 在
在![]() 上單調遞減,
上單調遞減,
因為![]() ,
, ![]() 趨近于0時,
趨近于0時, ![]() 趨向于
趨向于![]() ,且
,且![]() 時,
時, ![]() ,
,
由題意知,需![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() .
.
綜上知, 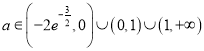 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分別為PC、PD、BC、PA的中點.
求證:(1)PA∥平面EFG;
(2)DH⊥平面EFG.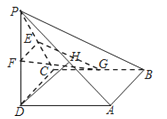
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫學院欲研究晝夜溫差大小與患感冒人數多少之間的關系,該協會分別到氣象局與某醫院抄錄了1到6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到數據資料見下表:

該院確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗.
(Ⅰ)求選取的2組數據恰好是不相鄰的兩個月的概率;
(Ⅱ)已知選取的是1月與6月的兩組數據.
(1)請根據2到5月份的數據,求出就診人數![]() 關于晝夜溫差
關于晝夜溫差![]() 的線性回歸方程;
的線性回歸方程;
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該協會所得線性回歸方程是否理想?
(參考公式和數據: 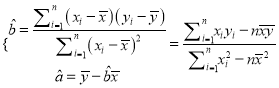
![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間計劃每天生產卡車模型、賽車模型、小汽車模型這三種玩具共100個,已知生產一個卡車模型需5分鐘,生產一個賽車模型需7分鐘,生產一個小汽車模型需4分鐘,且生產一個卡車模型可獲利潤8元,生產一個賽車模型可獲利潤9元,生產一個小汽車模型可獲利潤6元.若總生產時間不超過10小時,該公司合理分配生產任務使每天的利潤最大,則最大利潤是______________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C經過點![]() ,且圓心
,且圓心![]() 在直線
在直線![]() 上,又直線
上,又直線![]() 與圓C交于P,Q兩點.
與圓C交于P,Q兩點.
(1)求圓C的方程;
(2)若![]() ,求實數
,求實數![]() 的值;
的值;
(3)過點![]() 作直線
作直線![]() ,且
,且![]() 交圓C于M,N兩點,求四邊形
交圓C于M,N兩點,求四邊形![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與拋物線
與拋物線![]() 相切,且與
相切,且與![]() 軸的交點為
軸的交點為![]() ,點
,點![]() .若動點
.若動點![]() 與兩定點
與兩定點![]() 所構成三角形的周長為6.
所構成三角形的周長為6.
(Ⅰ) 求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ) 設斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,當
兩點,當![]() ,且
,且![]() 位于直線
位于直線![]() 的兩側時,證明:
的兩側時,證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正方體ABCD﹣A1B1C1D1的棱長為8cm,M,N,P分別是AB,A1D1 , BB1的中點.
(1)畫出過M,N,P三點的平面與平面A1B1C1D1的交線以及與平面BB1C1C的交線;
(2)設過M,N,P三點的平面與B1C1交于Q,求PQ的長.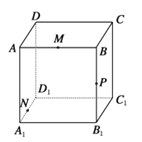
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某漁業公司今年年初用98萬元購進一艘漁船用于捕撈,第一年需要各種費用12萬元.從第二年起包括維修費在內每年所需費用比上一年增加4萬元.該船每年捕撈總收入50萬元.
(1)問捕撈幾年后總盈利最大,最大是多少?
(2)問捕撈幾年后的平均利潤最大,最大是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com