Question

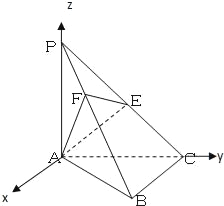
【題目】已知在三棱錐P﹣ABC中，PA⊥面ABC，AC⊥BC，且PA=AC=BC=1，點E是PC的中點，作EF⊥PB交PB于點F．

（Ⅰ）求證：PB⊥平面AEF；

（Ⅱ）求二面角A﹣PB﹣C的大小．

Answer 1

【答案】（Ⅰ）見解析；（2）60°．

【解析】試題分析：

（Ⅰ）要證直線PB與平面AEF垂直，就要證PB與平面AEF內兩條相交直線垂直，其中已知有一個垂直：EF⊥PB，由等腰三角形性質知AE⊥PC，因此可先證AE⊥平面PBC得AE⊥PB，這又可通過證明BC⊥平面PAC得到；（Ⅱ）要求二面角大小，由圖可建立空間直角坐標系（見解析），寫出各點坐標，求出二面角兩個面的法向量，由法向量夾角得二面角（相等或互補）．

試題解析：

（Ⅰ）證明：∵PA⊥面ABC，BC面ABC，

∴PA⊥BC，又AC⊥BC，PA⊥BC，PA∩AC=A，∴BC⊥面PAC，

而AEPAC，∴BC⊥AE，又PA=AC，點E是PC的中點，∴AE⊥PC，

又AE⊥BC，BC∩PC=C，∴AE⊥面PBC，而PB面PBC，AE⊥PB，又EF⊥PB，AE⊥BP，AE∩EF=E，∴PB⊥平面AEF；

（Ⅱ）解：以A為坐標原點，AC所在直線為y軸，AP所在直線為z軸建立空間直角坐標系，

∵PA=AC=BC=1，則A（0，0，0），P（0，0，1），C（0，1，0），B（1，1，0）．

．

設平面PAB的一個法向量為，

則由，得，取y1=﹣1，得x1=1，z1=0，

∴．

再設平面PBC的一個法向量為，

則由，得，取z2=1，得y2=1，

∴．

∴．

∴二面角A﹣PB﹣C的大小為60°．