
【題目】設數列 ![]() 的前
的前![]() 項和為
項和為![]() ,對一切
,對一切![]() ,點
,點![]() 都在函數
都在函數![]() 的圖象上.
的圖象上.
(1)求![]() ,歸納數列
,歸納數列![]() 的通項公式(不必證明);
的通項公式(不必證明);
(2)將數列![]() 依次按1項、2項、3項、4項循環地分為
依次按1項、2項、3項、4項循環地分為![]() ,
,![]() ,
,![]() ,
, ![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為
,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為![]() ,求
,求![]() 的值;
的值;
(3)設![]() 為數列
為數列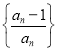 的前
的前![]() 項積,若不等式
項積,若不等式![]() 對一切
對一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]()
![]() ,
,![]() ,
,![]() ;(2)2010;(3)
;(2)2010;(3)![]() .
.
【解析】
(1)點![]() 坐標代入函數解析式,得
坐標代入函數解析式,得![]() ,令依次
,令依次![]() 可求得
可求得![]() ,歸納出通項公式;
,歸納出通項公式;
(2)依題意,每一次循環記為一組.由于每一個循環含有4個括號,故![]() 是第25組中第4個括號內各數之和.這樣可求得
是第25組中第4個括號內各數之和.這樣可求得![]() (注意規律),而
(注意規律),而![]() ,因此結論易用得.
,因此結論易用得.
(3)由![]() ,得
,得![]() ,不等式
,不等式![]() 對一切
對一切![]() 都成立, 就是
都成立, 就是![]() 對一切
對一切![]() 都成立,
都成立,
設![]() ,則只需
,則只需![]() 即可.用作商的方法說明
即可.用作商的方法說明![]() 是遞減數列,從而問題易求解.
是遞減數列,從而問題易求解.
(1)因為點![]() 在函數
在函數![]() 的圖象上,故
的圖象上,故![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() ,所以
,所以![]() ;令
;令![]() ,得
,得![]() ,所以
,所以![]() ,
,![]() ,……
,……
由此猜想:![]() .
.
(2)因為![]() ,所以數列
,所以數列![]() 依次按1項、2項、3項、4項循環地分為(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….
依次按1項、2項、3項、4項循環地分為(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….
每一次循環記為一組.由于每一個循環含有4個括號,故![]() 是第25組中第4個括號內各數之和.由分組規律知,由各組第4個括號中所有第1個數組成的數列是等差數列,且公差為20.
是第25組中第4個括號內各數之和.由分組規律知,由各組第4個括號中所有第1個數組成的數列是等差數列,且公差為20.
同理,由各組第4個括號中所有第2個數、所有第3個數、所有第4個數分別組成的數列也都是等差數列,且公差均為20. 故各組第4個括號中各數之和構成等差數列,且公差為80.
注意到第一組中第4個括號內各數之和是68,
所以![]() .又
.又![]() ,所以
,所以![]() .
.
(3)因為![]() ,故
,故![]() ,所以
,所以![]() .
.
又![]() ,故
,故![]() 對一切
對一切![]() 都成立,
都成立,
就是![]() 對一切
對一切![]() 都成立,
都成立,
設![]() ,則只需
,則只需![]() 即可.
即可.
由于 ,所以
,所以![]() ,故
,故![]() 是單調遞減,
是單調遞減,
于是![]() ,解得
,解得![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x-![]() ,x∈(0,1].
,x∈(0,1].
(1)當a=-1時,求函數y=f(x)的值域;
(2)若函數y=f(x)在x∈(0,1]上是減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是
是![]() 上的偶函數,對于
上的偶函數,對于![]() 都有
都有![]() 成立,且
成立,且![]() ,當
,當![]() ,
,![]() ,且
,且![]() 時,都有
時,都有![]() .則給出下列命題:①
.則給出下列命題:①![]() ;②
;②![]() 為函數
為函數![]() 圖象的一條對稱軸;③函數
圖象的一條對稱軸;③函數![]() 在
在![]() 上為減函數;④方程
上為減函數;④方程![]() 在
在![]() 上有4個根;其中正確的命題個數為( )
上有4個根;其中正確的命題個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓方程為![]() .
.
(1)設橢圓的左右焦點分別為![]() 、
、![]() ,點
,點![]() 在橢圓上運動,求
在橢圓上運動,求![]() 的值;
的值;
(2)設直線![]() 和圓
和圓![]() 相切,和橢圓交于
相切,和橢圓交于![]() 、
、![]() 兩點,
兩點,![]() 為原點,線段
為原點,線段![]() 、
、![]() 分別和圓
分別和圓![]() 交于
交于![]() 、
、![]() 兩點,設
兩點,設![]() 、
、![]() 的面積分別為
的面積分別為![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設甲、乙兩位同學上學期間,每天7:30之前到校的概率均為![]() .假定甲、乙兩位同學到校情況互不影響,且任一同學每天到校情況相互獨立.
.假定甲、乙兩位同學到校情況互不影響,且任一同學每天到校情況相互獨立.
(Ⅰ)用![]() 表示甲同學上學期間的三天中7:30之前到校的天數,求隨機變量
表示甲同學上學期間的三天中7:30之前到校的天數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)設![]() 為事件“上學期間的三天中,甲同學在7:30之前到校的天數比乙同學在7:30之前到校的天數恰好多2”,求事件
為事件“上學期間的三天中,甲同學在7:30之前到校的天數比乙同學在7:30之前到校的天數恰好多2”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于項數為m(![]() 且
且![]() )的有窮正整數數列
)的有窮正整數數列![]() ,記
,記![]()
![]() ,即
,即![]() 為
為![]() 中的最小值,設由
中的最小值,設由![]() 組成的數列
組成的數列![]() 稱為
稱為![]() 的“新型數列”.
的“新型數列”.
(1)若數列![]() 為2019,2020,2019,2018,2017,請寫出
為2019,2020,2019,2018,2017,請寫出![]() 的“新型數列”
的“新型數列”![]() 的所有項;
的所有項;
(2)若數列![]() 滿足
滿足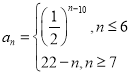 ,且其對應的“新型數列”
,且其對應的“新型數列”![]() 項數
項數![]() ,求
,求![]() 的所有項的和;
的所有項的和;
(3)若數列![]() 的各項互不相等且所有項的和等于所有項的積,求符合條件的
的各項互不相等且所有項的和等于所有項的積,求符合條件的![]() 及其對應的“新型數列”
及其對應的“新型數列”![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
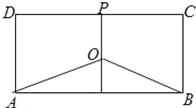
【題目】節能環保日益受到人們的重視,水污染治理也已成為“十三五”規劃的重要議題.某地有三家工廠,分別位于矩形![]() 的兩個頂點
的兩個頂點![]() 、
、![]() 及
及![]() 的中點
的中點![]() 處,
處,![]() ,
,![]() ,為了處理三家工廠的污水,現要在該矩形區域上(含邊界),且與
,為了處理三家工廠的污水,現要在該矩形區域上(含邊界),且與![]() 、
、![]() 等距離的一點
等距離的一點![]() 處,建造一個污水處理廠,并鋪設三條排污管道
處,建造一個污水處理廠,并鋪設三條排污管道![]() 、
、![]() 、
、![]() .設
.設![]() ∠BAO=x(弧度),排污管道的總長度為
∠BAO=x(弧度),排污管道的總長度為![]() .
.
(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)試確定![]() 點的位置,使鋪設的排污管道的總長度最短,并求總長度的最短公里數(精確到
點的位置,使鋪設的排污管道的總長度最短,并求總長度的最短公里數(精確到![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com