
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調減區間;
的單調減區間;
(2)若不等式![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,試問過點
時,試問過點![]() 可作
可作![]() 的幾條切線?并說明理由.
的幾條切線?并說明理由.
【答案】(1)單調減區間為![]() (2)
(2)![]() (3)當
(3)當![]() 時,切線有一條;當
時,切線有一條;當![]() 時,切線有兩條,詳見解析
時,切線有兩條,詳見解析
【解析】
(1)對![]() 求導得到
求導得到![]() ,令
,令![]() ,得到
,得到![]() 的范圍,從而得到
的范圍,從而得到![]() 的單調區間;
的單調區間;
(2)令![]() ,求導得到
,求導得到![]() ,令
,令![]() ,分
,分![]() ,
,![]() ,
,![]() ,研究
,研究![]() 的正負,即
的正負,即![]() 的正負,從而得到
的正負,從而得到![]() 的單調性,再判斷
的單調性,再判斷![]() 與
與![]() 的關系,從而得到
的關系,從而得到![]() 的范圍;
的范圍;
(3)切點為![]() ,利用導數的幾何意義表示出過
,利用導數的幾何意義表示出過![]() 的切線,代入
的切線,代入![]() 點坐標得到
點坐標得到![]() ,令
,令![]() ,分
,分![]() ,
,![]() 討論
討論![]() 的正負,從而得到
的正負,從而得到![]() 的單調性,再研究其零點,從而得到切點的個數和切線的條數.
的單調性,再研究其零點,從而得到切點的個數和切線的條數.
解:(1)![]() 時,
時,![]() ,
,
![]() ,
,
令![]() ,則
,則![]() ,所以
,所以![]() 的單調減區間為
的單調減區間為![]() .
.
(2)令![]() ,
,
![]() ,
,
令![]() ,∵
,∵![]() ,又
,又![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 成立;
成立;
②當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
∴![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 成立;
成立;
③當![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上有唯一零點,記為
上有唯一零點,記為![]() ,
,
且![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
∴當![]() 時,
時,![]() ,不成立.
,不成立.
綜上:![]() .
.
(3)設過![]() 的切線的切點為
的切線的切點為![]() ,則
,則![]() ,
,
切線方程為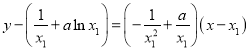 ,
,
又切線過![]() ,得
,得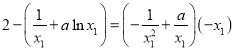 ,
,
即![]() ,
,
令![]() ,
,![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上遞減,
上遞減,
由![]() ,
,![]() ,
,
所以![]() 只有一解,即切線只有一條;
只有一解,即切線只有一條;
②當![]() 時,令
時,令![]() ,
,![]() ,
,
由![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 遞增,
遞增,
又![]() ,所以
,所以![]() ,
,
一方面:∵![]() ,
,
∵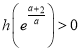 ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 在
在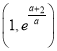 上有零點;
上有零點;
另一方面:由(2)知![]() 對
對![]() 恒成立,
恒成立,
∴![]() 對
對![]() 恒成立,
恒成立,
∴當![]() 時,有
時,有
![]() ,
,
∴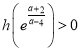 ,又
,又![]() 時,
時,![]() ,∴
,∴![]() ,
,
∴![]() 在
在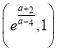 上有零點,故
上有零點,故![]() 有兩個零點,即切線有兩條.
有兩個零點,即切線有兩條.
綜上,當![]() 時,切線有一條;當
時,切線有一條;當![]() 時,切線有兩條.
時,切線有兩條.


科目:高中數學 來源: 題型:
【題目】設函數![]() (a,b
(a,b![]() R).
R).
(1)當b=﹣1時,函數![]() 有兩個極值,求a的取值范圍;
有兩個極值,求a的取值范圍;
(2)當a+b=1時,函數![]() 的最小值為2,求a的值;
的最小值為2,求a的值;
(3)對任意給定的正實數a,b,證明:存在實數![]() ,當
,當![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2019年亞洲杯前,某商家為了鼓勵中國球迷組團到阿聯酋支持中國隊,制作了3種精美海報,每份中國隊球迷禮包中隨機裝入一份海報,每集齊3種不同的海報就可獲得中國隊在亞洲杯上所有比賽中的1張門票.現有6名中國隊球迷組成的球迷團,每人各買一份中國隊球迷禮包,則該球迷團至少獲得1張門票的可能情況的種數為( )
A.360B.450C.540D.990
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以原點
為參數),以原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸建立極坐標系,曲線
軸非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設點![]() ,
,![]() 分別是曲線
分別是曲線![]() ,
,![]() 上兩動點且
上兩動點且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
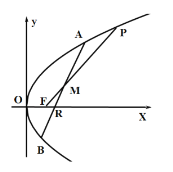
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,點
的焦點,點![]() 在拋物線
在拋物線![]() 上,過點
上,過點![]() 的直線交拋物線
的直線交拋物線![]() 于
于![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,且滿足
,且滿足![]() .
.
(1)若直線![]() 的斜率為1,求點
的斜率為1,求點![]() 的坐標;
的坐標;
(2)若![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線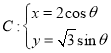 (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程
的極坐標方程![]() ,點
,點![]() 在直線
在直線![]() 上,直線
上,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求曲線![]() 的普通方程及直線
的普通方程及直線![]() 的參數方程;
的參數方程;
(2)求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com