【題目】
的內角
的對邊分別為
，已知
(1)求
；
(2)若
，求
面積的最大值.
【答案】(1)
；(2)
.
【解析】試題分析：(1)由正弦定理及兩角和的正弦公式,三角形內角和公式可得
,進而得；(2)由余弦定理可得
,由基本不等式,得
,代入三角形面積公式,可得三角形面積的最大值.
試題解析： (1)因為
所以由正弦定理得
...........................2分
所以
即
.....................3分
因為
，所以，又
，解得...................5分；
(2)由余弦定理得
，即...................6分
由不等式得
，當且僅當
時，取等號，所以
，
解得...................8分
所以
的面積為
所以面積的最大值為...................10分.
科目：高中數學 來源： 題型：
【題目】某企業生產A，B兩種產品，生產1噸A種產品需要煤4噸、電18千瓦；生產1噸B種產品需要煤1噸、電15千瓦。現因條件限制，該企業僅有煤10噸，并且供電局只能供電66千瓦，若生產1噸A種產品的利潤為10000元；生產1噸B種產品的利潤是5000元，試問該企業如何安排生產，才能獲得最大利潤？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為了了解一年內的用水情況，抽取了10天的用水量如下表所示：
天數 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量／噸 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
（Ⅰ）在這10天中，該公司用水量的平均數是多少？每天用水量的中位數是多少？
（Ⅱ）你認為應該用平均數和中位數中的哪一個數來描述該公司每天的用水量？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量
．
(1)若
分別表示將一枚質地均勻的正方體骰子（六個面的點數分別為1,2,3,4,5,6）先后拋擲兩次時第一次、第二次出現的點數，求滿足
的概率；
(2)若在連續區間
上取值，求滿足
的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，圓
的參數方程為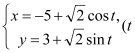
為參數），在以原點
為極點，
軸的非負半軸為極軸建立的極坐標系中，直線
的極坐標方程為
.
（1）求圓
的普通方程和直線
的直角坐標方程；
（2）設直線
與
軸，
軸分別交于
兩點，點
是圓
上任一點，求
兩點的極坐標和
面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4—4：坐標系與參數方程
已知平面直角坐標系
，以
為極點，
軸的非負半軸為極軸建立極坐標系，
點的極坐標為
，曲線
的參數方程為
（
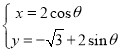為參數）.
（1）寫出點
的直角坐標及曲線
的直角坐標方程；
（2）若
為曲線
上的動點，求
中點
到直線
的距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了保護環境，2015年合肥市勝利工廠在市政府的大力支持下，進行技術改進：把二氧化碳轉化為某種化工產品，經測算，該處理成本
（萬元）與處理量
（噸）之間的函數關系可近似地表示為：
且每處理一噸二氧化碳可得價值為20萬元的某種化工產品．
（1）當
時，判斷該技術改進能否獲利？如果能獲利，求出最大利潤；如果不能獲利，則國家至少需要補貼多少萬元，該工廠才不虧損？
（2）當處理量為多少噸時，每噸的平均處理成本最少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
