【題目】如圖，將長為4，寬為1的長方形折疊成長方體ABCD-A1B1C1D1的四個側面，記底面上一邊
，連接A1B,A1C,A1D.
（1）求長方體ABCD-A1B1C1D1體積的最大值 ；
（2）當長方體ABCD-A1B1C1D1的體積最大時，求二面角B-A1C-D的大小.
【答案】(1)1;(2)
【解析】
（1）用
表示出長方體ABCD-A1B1C1D1體積為：
，
，求該二次函數類型函數的最大值即可。
（2）由（1）得
時，長方體ABCD-A1B1C1D1體積最大，此時該幾何體為正方體，過點
作
垂直A1C于點E，連接ED，則
就是二面角B-A1C-D的一個平面角，解三角形
即可。
（1）長方體ABCD-A1B1C1D1體積為：，，當時，
，所以長方體ABCD-A1B1C1D1體積的最大值為1.
（2）由（1）得時，長方體ABCD-A1B1C1D1體積最大，此時該幾何體為正方體，過點作垂直A1C于點E，連接ED，
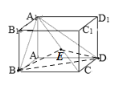
由正方體可得：
,所以就是二面角B-A1C-D的一個平面角，
在正方體ABCD-A1B1C1D1中可得：
，
，
在三角形由余弦定理得：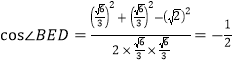
所以
通城學典默寫能手系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】2018年9月16日下午5時左右，今年第22號臺風“山竹”在廣東江門川島鎮附近正面登陸，給當地人民造成了巨大的財產損失，某記者調查了當地某小區的100戶居民由于臺風造成的經濟損失，將收集的數據分成
，
，
，
，
五組，并作出如下頻率分布直方圖.
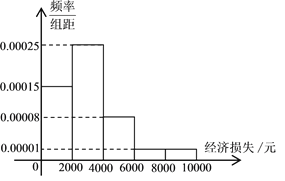
（Ⅰ）根據頻率分布直方圖估計該小區居民由于臺風造成的經濟損失的眾數和平均值.
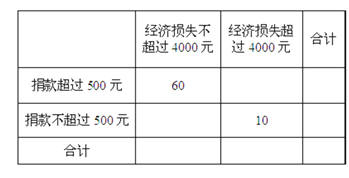
（Ⅱ）“一方有難，八方支援”，臺風后居委會號召小區居民為臺風重災區捐款，
記者調查的100戶居民捐款情況如下表格，在如圖表格空白處填寫正確數字，并說明是否有99%以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關？
參考公式：
，其中
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，點
在傾斜角為
的直線
上，以坐標原點
為極點，以
軸正半軸為極軸，建立極坐標系，曲線
的方程為
.
（1）寫出
的參數方程及
的直角坐標方程；
（2）設
與
相交于
兩點，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在
上的函數
,其導函數
的大致圖像如圖所示,則下列敘述正確的是().
（1）
（2）函數在
上遞增，在
上遞減
（3）的極值點為c，e
（4）的極大值為
A. (1)(2) B. (2)(3) C. (3) D. (1)(4)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
是定義在
上的偶函數，且當
時， 
．現已畫出函數
在
軸左側的圖象，如圖所示，并根據圖象：
（1）直接寫出函數
， 
的增區間；
（2）寫出函數
， 
的解析式；
（3）若函數
， 
，求函數
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正方體ABCD-A1B1C1D1的棱長為2，E為棱CC1的中點，點M在正方形BCC1B1內運動，且直線AM//平面A1DE,則動點M 的軌跡長度為（ ）
A. 
B. π C. 2 D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
