
【題目】本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分.
從數列![]() 中取出部分項,并將它們按原來的順序組成一個數列,稱之為數列
中取出部分項,并將它們按原來的順序組成一個數列,稱之為數列![]() 的一個子數列.
的一個子數列.
設數列![]() 是一個首項為
是一個首項為![]() 、公差為
、公差為![]()
![]() 的無窮等差數列.
的無窮等差數列.
(1)若![]() ,
,![]() ,
,![]() 成等比數列,求其公比
成等比數列,求其公比![]() .
.
(2)若![]() ,從數列
,從數列![]() 中取出第2項、第6項作為一個等比數列的第1項、第2項,試問該數列是否為
中取出第2項、第6項作為一個等比數列的第1項、第2項,試問該數列是否為![]() 的無窮等比子數列,請說明理由.
的無窮等比子數列,請說明理由.
(3)若![]() ,從數列
,從數列![]() 中取出第1項、第
中取出第1項、第![]()
![]() 項(設
項(設![]() )作為一個等比數列的第1項、第2項,試問當且僅當
)作為一個等比數列的第1項、第2項,試問當且僅當![]() 為何值時,該數列為
為何值時,該數列為![]() 的無窮等比子數列,請說明理由.
的無窮等比子數列,請說明理由.
【答案】略
【解析】
(1)由題設,得![]() ,即
,即![]() ,得
,得![]() ,又
,又![]() ,于是
,于是![]() ,故其公比
,故其公比![]() .(4分)
.(4分)
(2)設等比數列為![]() ,其公比
,其公比![]() ,
,![]() ,(6分)
,(6分)
由題設![]() .
.
假設數列![]() 為
為![]() 的無窮等比子數列,則對任意自然數
的無窮等比子數列,則對任意自然數![]()
![]() ,都存在
,都存在![]() ,使
,使![]() ,
,
即![]() ,得
,得![]() ,(8分)
,(8分)
當![]() 時,
時,![]() ,與假設矛盾,
,與假設矛盾,
故該數列不為![]() 的無窮等比子數列.(10分)
的無窮等比子數列.(10分)
(3)①設![]() 的無窮等比子數列為
的無窮等比子數列為![]() ,其公比
,其公比![]() (
(![]() ),得
),得![]() ,
,
由題設,在等差數列![]() 中,
中,![]() ,
,![]() ,
,
因為數列![]() 為
為![]() 的無窮等比子數列,所以對任意自然數
的無窮等比子數列,所以對任意自然數![]()
![]() ,都存在
,都存在![]() ,使
,使![]() ,
,
即![]() ,得
,得![]() ,
,
由于上式對任意大于等于![]() 的正整數
的正整數![]() 都成立,且
都成立,且![]() ,
,![]() 均為正整數,
均為正整數,
可知![]() 必為正整數,又
必為正整數,又![]() ,故
,故![]() 是大于1的正整數.(14分)
是大于1的正整數.(14分)
②再證明:若![]() 是大于1的正整數,則數列
是大于1的正整數,則數列![]() 存在無窮等比子數列.
存在無窮等比子數列.
即證明無窮等比數列![]() 中的每一項均為數列
中的每一項均為數列![]() 中的項.
中的項.
在等比數列![]() 中,
中,![]() ,
,
在等差數列![]() 中,
中,![]() ,
,![]() ,
,
若![]() 為數列
為數列![]() 中的第
中的第![]() 項,則由
項,則由![]() ,得
,得![]() ,整理得
,整理得![]() ,
,
由![]() ,
,![]() 均為正整數,得
均為正整數,得![]() 也為正整數,
也為正整數,
故無窮等比數列![]() 中的每一項均為數列
中的每一項均為數列![]() 中的項,得證.
中的項,得證.
綜上,當且僅當![]() 是大于1的正整數時,數列
是大于1的正整數時,數列![]() 存在無窮等比子數列.(18分)
存在無窮等比子數列.(18分)


科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() .點
.點![]() 、
、![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 、
、![]() 的中點,
的中點,![]() 是線段
是線段![]() 的中點,
的中點,![]() ,
,![]() .
.
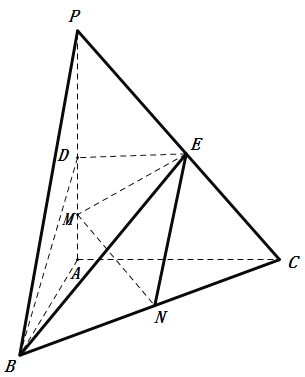
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知點![]() 在棱
在棱![]() 上,且直線
上,且直線![]() 與直線
與直線![]() 所成角的余弦值為
所成角的余弦值為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某土特產超市為預估2020年元旦期間游客購買土特產的情況,對2019年元旦期間的90位游客購買情況進行統計,得到如下人數分布表.
購買金額(元) |
|
|
|
|
|
|
人數 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根據以上數據完成![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為購買金額是否少于60元與性別有關.
的把握認為購買金額是否少于60元與性別有關.
不少于60元 | 少于60元 | 合計 | |
男 | 40 | ||
18 | |||
合計 |
(2)為吸引游客,該超市推出一種優惠方案,購買金額不少于60元可抽獎3次,每次中獎概率為![]() (每次抽獎互不影響,且
(每次抽獎互不影響,且![]() 的值等于人數分布表中購買金額不少于60元的頻率),中獎1次減5元,中獎2次減10元,中獎3次減15元.若游客甲計劃購買80元的土特產,請列出實際付款數
的值等于人數分布表中購買金額不少于60元的頻率),中獎1次減5元,中獎2次減10元,中獎3次減15元.若游客甲計劃購買80元的土特產,請列出實際付款數![]() (元)的分布列并求其數學期望.
(元)的分布列并求其數學期望.
附:參考公式和數據: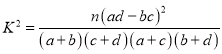 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在棱長為2的正方體![]() 中,點
中,點![]() 是對角線
是對角線![]() 上的點(點
上的點(點![]() 與
與![]() 、
、![]() 不重合),則下列結論正確的個數為( )
不重合),則下列結論正確的個數為( )
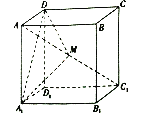
①存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
③若![]() 的面積為
的面積為![]() ,則
,則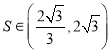 ;
;
④若![]() 、
、![]() 分別是
分別是![]() 在平面
在平面![]() 與平面
與平面![]() 的正投影的面積,則存在點
的正投影的面積,則存在點![]() ,使得
,使得![]() .
.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點列![]() 為函數
為函數![]() 圖像上的點,點列
圖像上的點,點列![]() 順次為
順次為![]() 軸上的點,其中
軸上的點,其中![]() ,對任意
,對任意![]() ,點
,點![]() 構成以
構成以![]() 為頂點的等腰三角形.
為頂點的等腰三角形.
(1)證明:數列![]() 是等比數列;
是等比數列;
(2)若數列![]() 中任意連續三項能構成三角形的三邊,求
中任意連續三項能構成三角形的三邊,求![]() 的取值范圍;
的取值范圍;
(3)求證:對任意![]() ,
,![]() 是常數,并求數列
是常數,并求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個半圓中有兩個互切的內切半圓,由三個半圓弧圍成曲邊三角形,作兩個內切半圓的公切線把曲邊三角形分隔成兩塊,阿基米德發現被分隔的這兩塊的內切圓是同樣大小的,由于其形狀很像皮匠用來切割皮料的刀子,他稱此為“皮匠刀定理”,如圖,若![]() ,則陰影部分與最大半圓的面積比為( )
,則陰影部分與最大半圓的面積比為( )
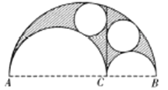
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點,
的中點,![]() 為線段
為線段![]() 上的動點.
上的動點.
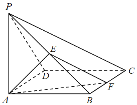
(1)求證:平面![]() 平面
平面![]() .
.
(2)試確定點![]() 的位置,使平面
的位置,使平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com