
【題目】某廠為了解甲、乙兩條生產線生產的產品的質量,從兩條生產線生產的產品中隨機抽取各10件,測量產品中某種元素的含量(單位:毫克).如圖是測量數據的莖葉圖:
規定:當產品中的此種元素含量滿足≥18毫克時,該產品為優等品.
(1)根據樣本數據,計算甲、乙兩條生產線產品質量的均值與方差,并說明哪條生產線的產品的質量相對穩定;
(2)從乙廠抽出的上述10件產品中,隨機抽取3件,求抽到的3件產品中優等品數ξ的分布列及其數學期望E(ξ).
【答案】
(1)解:設甲、乙兩個車間產品某種元素含量的均值分別為 ![]() 、
、 ![]() ,方差分別為
,方差分別為 ![]() 、
、 ![]() ,
,
![]() =
= ![]() ,
,
![]() =
= ![]()
![]() =
= ![]() [(9﹣18)2+(13﹣18)2+(19﹣18)2+(16﹣18)2+(15﹣18)2+(18﹣18)2+(21﹣18)2+(25﹣18)2+(21﹣18)2+(23﹣18)2]=14,
[(9﹣18)2+(13﹣18)2+(19﹣18)2+(16﹣18)2+(15﹣18)2+(18﹣18)2+(21﹣18)2+(25﹣18)2+(21﹣18)2+(23﹣18)2]=14,
![]() =
= ![]() [(18﹣18)2+(16﹣18)2+(17﹣18)2+(16﹣18)2+(19﹣18)2+(12﹣18)2+(15﹣18)2+(22﹣18)2+(21﹣18)2+(24﹣18)2]=11.6,
[(18﹣18)2+(16﹣18)2+(17﹣18)2+(16﹣18)2+(19﹣18)2+(12﹣18)2+(15﹣18)2+(22﹣18)2+(21﹣18)2+(24﹣18)2]=11.6,
∵ ![]() =
= ![]() ,
, ![]() ,∴乙生產線的產品的質量相對穩定.
,∴乙生產線的產品的質量相對穩定.
(2)解:由樣本數據可知,乙廠10件產品中有5件是優等品,
∴ξ的取值為0,1,2,3.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴ξ的分布列為:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故ξ的數學期望為 ![]() .
.
【解析】(1)分別求出甲、乙兩個車間產品某種元素含量的均值 ![]() 、
、 ![]() ,方差
,方差 ![]() 、
、 ![]() ,由
,由 ![]() =
= ![]() ,
, ![]() ,知乙生產線的產品的質量相對穩定.(2)由樣本數據可知,乙廠10件產品中有5件是優等品,ξ的取值為0,1,2,3.分別求出相應的概率,由此能求出ξ的分布列和數學期望.
,知乙生產線的產品的質量相對穩定.(2)由樣本數據可知,乙廠10件產品中有5件是優等品,ξ的取值為0,1,2,3.分別求出相應的概率,由此能求出ξ的分布列和數學期望.
【考點精析】掌握莖葉圖是解答本題的根本,需要知道莖葉圖又稱“枝葉圖”,它的思路是將數組中的數按位數進行比較,將數的大小基本不變或變化不大的位作為一個主干(莖),將變化大的位的數作為分枝(葉),列在主干的后面,這樣就可以清楚地看到每個主干后面的幾個數,每個數具體是多少.


科目:高中數學 來源: 題型:
【題目】設函數f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的導函數.
(1)若f(x)≥ag(x)恒成立,求實數a的取值范圍;
(2)設n∈N* , 證明: ![]() +
+ ![]() +…+
+…+ ![]() <ln(n+1).
<ln(n+1).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C1:(x﹣1)2+(y﹣3)2=1,圓C2:(x﹣6)2+(y﹣1)2=1,M,N分別是圓C1 , C2上的動點,P為直線x﹣y﹣2=0上的動點,則||PM|﹣|PN||的最大值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓Γ: ![]() +
+ ![]() =1(a>b>0)的右焦點與短軸兩端點構成一個面積為2的等腰直角三角形,O為坐標原點:
=1(a>b>0)的右焦點與短軸兩端點構成一個面積為2的等腰直角三角形,O為坐標原點: 
(1)求橢圓Г的方程:
(2)設點A在橢圓Г上,點B在直線y=2上,且OA⊥OB,求證: ![]() +
+ ![]() 為定值:
為定值:
(3)設點C在Γ上運動,OC⊥OD,且點O到直線CD距離為常數d(0<d<2),求動點D的軌跡方程:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某學校高三年級共800名男生中隨機抽取50人測量身高.數據表明,被測學生身高全部介于155cm到195cm之間,將測量結果按如下方式分成八組:第一組[155,160);第二組[160,165);…;第八組[190,195].如圖是按上述分組方法得到的頻率分布直方圖的一部分.已知第一組與第八組人數相同,第六組比第七組少1人. 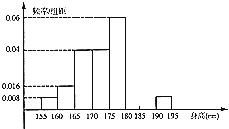
(1)估計這所學校高三年級全體男生身高在180cm以上(含180cm)的人數;
(2)若從身高屬于第六組和第八組的所有男生中隨機抽取兩人,記他們的身高分別為x,y,求滿足“|x﹣y|≤5”的事件的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com