
已知角A、B、C為△ABC的三個(gè)內(nèi)角,其對(duì)邊分別為a、b、c,若 =(-cos
=(-cos ,sin
,sin ),
), =(cos
=(cos ,sin
,sin ),a=2
),a=2 ,且
,且 ·
· =
= .
.
(1)若△ABC的面積S= ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范圍.
(1)4;(2)(2 ,4]
,4]
解析試題分析:(1)由 =(-cos
=(-cos ,sin
,sin ),
), =(cos
=(cos ,sin
,sin ),且
),且 ·
· =
= .可求得角A的值,又因?yàn)椤鰽BC的面積S=
.可求得角A的值,又因?yàn)椤鰽BC的面積S= ,a=2
,a=2 ,在三角形中利用余弦與三角形的面積公式,即可解出b,c的值或者直接構(gòu)造b+c,即可得到結(jié)論.
,在三角形中利用余弦與三角形的面積公式,即可解出b,c的值或者直接構(gòu)造b+c,即可得到結(jié)論.
(2)由(1)可知角A,以及邊長(zhǎng) .用角B結(jié)合正弦定理分別表示出b,c.再結(jié)合角B的范圍,求出b+c的取值范圍即可.
.用角B結(jié)合正弦定理分別表示出b,c.再結(jié)合角B的范圍,求出b+c的取值范圍即可.
(1)∵ =(-cos
=(-cos ,sin
,sin ),
), =(cos
=(cos ,sin
,sin ),且
),且 ·
· =
= ,
,
∴-cos2 +sin2
+sin2 =
= ,即-cosA=
,即-cosA= ,
,
又A∈(0,π),∴A=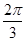 . …………3分
. …………3分
又由S△ABC= bcsinA=
bcsinA= ,所以bc=4,
,所以bc=4,
由余弦定理得:a2=b2+c2-2bc·cos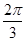 =b2+c2+bc,
=b2+c2+bc,
∴16=(b+c)2,故b+c=4.………7分
(2)由正弦定理得: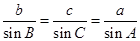 =
=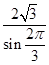 =4,又B+C=p-A=
=4,又B+C=p-A=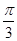 ,
,
∴b+c=4sinB+4sinC=4sinB+4sin(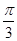 -B)=4sin(B+
-B)=4sin(B+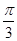 ), 12分
), 12分
∵0<B<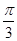 ,則
,則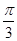 <B+
<B+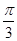 <
<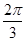 ,則
,則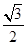 <sin(B+
<sin(B+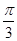 )≤1,即b+c的取值范圍是(2
)≤1,即b+c的取值范圍是(2 ,4]…..14分
,4]…..14分
考點(diǎn):1.三角函數(shù)恒等變換.2.正余弦定理的應(yīng)用.3.三角函數(shù)最值的求法.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知a、b、c分別是△ABC三個(gè)內(nèi)角A、B、C的對(duì)邊.
(1)若△ABC面積為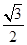 ,c=2,A=60º,求a,b的值;
,c=2,A=60º,求a,b的值;
(2)若acosA=bcosB,試判斷△ABC的形狀,證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) .
.
(1)設(shè) ,且
,且 ,求
,求 的值;
的值;
(2)在△ABC中,AB=1, ,且△ABC的面積為
,且△ABC的面積為 ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
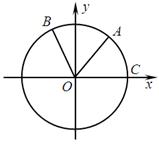
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,點(diǎn)A、B是單位圓 上的兩點(diǎn),點(diǎn)C是圓
上的兩點(diǎn),點(diǎn)C是圓 與
與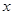 軸的正半軸的交點(diǎn),將銳角
軸的正半軸的交點(diǎn),將銳角 的終邊
的終邊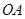 按逆時(shí)針方向旋轉(zhuǎn)
按逆時(shí)針方向旋轉(zhuǎn) 到
到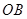 .
.
(1)若點(diǎn)A的坐標(biāo)為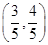 ,求
,求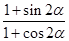 的值;
的值;
(2)用 表示
表示 ,并求
,并求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在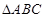 中,角A、B、C的對(duì)邊分別為a、b、c,且角A、B、C成等差教列.(1)若
中,角A、B、C的對(duì)邊分別為a、b、c,且角A、B、C成等差教列.(1)若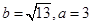 ,求邊c的值;
,求邊c的值;
(2)設(shè)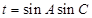 ,求t的最大值.
,求t的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com