
【題目】某校開設A、B、C、D、E五門選修課,要求每位同學彼此獨立地從中選修3門課程.某甲同學必選A課程,不選B課程,另從其余課程中隨機任選兩門課程.乙、丙兩名同學從五門課程中隨機任選三門課程.
(1)求甲同學選中C課程且乙、丙同學未選C課程的概率;
(2)用X表示甲、乙、丙選中C課程的人數之和,求X的分布列和數學期望.
【答案】
(1)解:設甲同學選中C課程為事件A,乙同學選中C課程為事件B,丙同學選中C課程為事件C,
甲同學選中C課程且乙、丙同學未選C課程為事件D,
由P(A)= ![]() =
= ![]() ,P(
,P( ![]() )=
)= ![]() =
= ![]() ,P(
,P( ![]() )=
)= ![]() =
= ![]() ,
,
由題意知每位同學選課彼此獨立,
∴甲同學選中C課程且乙、丙同學未選C課程的概率:
P(D)=P(A)P( ![]() )P(
)P( ![]() )=
)= ![]() =
= ![]()
(2)解:由題意得X的可能取值為0,1,2,3,
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
P(X=2)= ![]() +
+ ![]() =
= ![]() ,
,
P(X=3)= ![]() =
= ![]() .
.
則X的分布列為:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴數學期望E(X)= ![]() =
= ![]()
【解析】(1)設甲同學選中C課程為事件A,乙同學選中C課程為事件B,丙同學選中C課程為事件C,甲同學選中C課程且乙、丙同學未選C課程為事件D,由P(D)=P(A)P( ![]() )P(
)P( ![]() ),能求出甲同學選中C課程且乙、丙同學未選C課程的概率.(2)由題意得X的可能取值為0,1,2,3,分別求出相應的概率,由此能求出X的分布列和數學期望E(X).
),能求出甲同學選中C課程且乙、丙同學未選C課程的概率.(2)由題意得X的可能取值為0,1,2,3,分別求出相應的概率,由此能求出X的分布列和數學期望E(X).


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:
【題目】設b和c分別是先后拋擲一枚骰子得到的點數,用隨機變量ξ表示方程x2+bx+c=0實根的個數(重根按一個計).
(1)求方程x2+bx+c=0有實根的概率;
(2)求ξ的分布列和數學期望;
(3)求在先后兩次出現的點數中有5的條件下,方程x2+bx+c=0有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在多面體SP﹣ABCD中,底面ABCD為矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E為BC的中點.
(1)求證:AE∥面SPD;
(2)求三棱錐S-BPD的體積。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (x+
(x+ ![]() ),g(x)=
),g(x)= ![]() (x﹣
(x﹣ ![]() ).
).
(1)求函數h(x)=f(x)+2g(x)的零點;
(2)求函數F(x)=[f(x)]2n﹣[g(x)]2n(n∈N*)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在矩形ABCD中,對角線AC與相鄰兩邊所成的角為α,β,則cos2α+cos2β=1.類比到空間中一個正確命題是:在長方體ABCD﹣A1B1C1D1中,對角線AC1與相鄰三個面所成的角為α,β,γ,則有 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了檢驗學習情況,某培訓機構于近期舉辦一場競賽活動,分別從甲、乙兩班各抽取10名學員的成績進行統計分析,其成績的莖葉圖如圖所示(單位:分),假設成績不低于90分者命名為“優秀學員”.
(1)分別求甲、乙兩班學員成績的平均分(結果保留一位小數);
(2)從甲班4名優秀學員中抽取兩人,從乙班2名80分以下的學員中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,我市某居民小區擬在邊長為1百米的正方形地塊ABCD上劃出一個三角形地塊APQ種植草坪,兩個三角形地塊PAB與QAD種植花卉,一個三角形地塊CPQ設計成水景噴泉,四周鋪設小路供居民平時休閑散步,點P在邊BC上,點Q在邊CD上,記∠PAB=a. 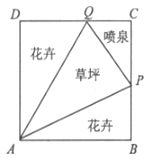
(1)當∠PAQ= ![]() 時,求花卉種植面積S關于a的函數表達式,并求S的最小值;
時,求花卉種植面積S關于a的函數表達式,并求S的最小值;
(2)考慮到小區道路的整體規劃,要求PB+DQ=PQ,請探究∠PAQ是否為定值,若是,求出此定值,若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com