Question

【題目】已知函數f（x）=lnx﹣a2x2+ax，a∈R，且a≠0．
（1）若函數f（x）在區間[1，+∞）上是減函數，求實數a的取值范圍；
（2）設函數g（x）=（3a+1）x﹣（a2+a）x2 ， 當x＞1時，f（x）＜g（x）恒成立，求a的取值范圍．

Answer 1

【答案】
（1）解：∵f（x）=lnx﹣a2x2+ax，其定義域為（0，+∞），

∴f′（x）= ﹣2a2x+a= = ．

①當a=0時，f′（x）= ＞0，

∴f（x）在區間（0，+∞）上為增函數，不合題意．

②當a＞0時，f′（x）＜0（x＞0）等價于（2ax+1）（ax﹣1）＞0（x＞0），即x＞ ．

此時f（x）的單調遞減區間為（ ，+∞）．

依題意，得 解之，得a≥1．

③當a＜0時，f′（x）＜0（x＞0）等價于（2ax+1）（ax﹣1）＞0（x＞0），即x＞﹣ ．

此時f（x）的單調遞減區間為（﹣ ，+∞）．

依題意，得 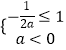解之，得a≤﹣ ．

綜上所述，實數a的取值范圍是（﹣∞，﹣ ]∪[1，+∞）

（2）解：∵g（x）=（3a+1）x﹣（a2+a）x2，

∴f（x）﹣g（x）=lnx﹣（2a+1）x+ax2＜0，

即lnx﹣x＜2ax﹣ax2，在（1，+∞）恒成立，

設h（x）=lnx﹣x，

則h′（x）= ﹣1＜0恒成立，

∴h（x）在（1，+∞）為減函數，

∴h（x）＜h（1）=﹣1，

∴ax2﹣2ax﹣1＜0，在（1，+∞）上恒成立，

設φ（x）=ax2﹣2ax﹣1

當a=0時，﹣1＜0，符合題意，

當a＞0時，顯然不滿足題意，

當a＜0，由于對稱軸x=1，則φ（1）＜0，即a﹣2a﹣1＜0，解得﹣1＜a＜0，

綜上所述，a的取值范圍為（﹣1，0]

【解析】（1）先求導，再分類討論，根據導數和函數的單調性的關系即可求出a的取值范圍，（2）當x＞1時，f（x）＜g（x）恒成立，轉化為lnx﹣x＜2ax﹣ax2 ， 在（1，+∞）恒成立，構造函數h（x）=lnx﹣x，利用導數求出函數最值，得到ax2﹣2ax﹣1＜0，在（1，+∞）上恒成立，再分類討論，根據二次函數的性質即可求出a的取值范圍．
【考點精析】本題主要考查了利用導數研究函數的單調性和函數的最大(小)值與導數的相關知識點，需要掌握一般的,函數的單調性與其導數的正負有如下關系： 在某個區間內，(1)如果，那么函數在這個區間單調遞增；(2)如果，那么函數在這個區間單調遞減；求函數在上的最大值與最小值的步驟：（1）求函數在內的極值；（2）將函數的各極值與端點處的函數值，比較，其中最大的是一個最大值，最小的是最小值才能正確解答此題．