
【題目】等邊三角形ABC與正方形ABDE有一公共邊AB,二面角C﹣AB﹣D的余弦值為 ![]() ,M,N分別是AC.BC的中點,則EM,AN所成角的余弦值等于( )
,M,N分別是AC.BC的中點,則EM,AN所成角的余弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:設AB=2,作CO⊥面ABDE, OH⊥AB,則CH⊥AB,∠CHO為二面角C﹣AB﹣D的平面角,
CH= ![]() ,OH=CHcos∠CHO=1,
,OH=CHcos∠CHO=1,
結合等邊三角形ABC與正方形ABDE可知此四棱錐為正四棱錐,
則AN=EM=CH= ![]() ,
, ![]() =
= ![]() (
( ![]() +
+ ![]() ),
), ![]() =
= ![]()
![]() ﹣
﹣ ![]() ,
,
∴ ![]() =
= ![]() .
.
故EM,AN所成角的余弦值 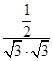 =
= ![]() ,
,
故選D.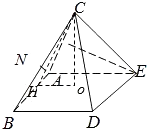
【考點精析】本題主要考查了異面直線及其所成的角的相關知識點,需要掌握異面直線所成角的求法:1、平移法:在異面直線中的一條直線中選擇一特殊點,作另一條的平行線;2、補形法:把空間圖形補成熟悉的或完整的幾何體,如正方體、平行六面體、長方體等,其目的在于容易發現兩條異面直線間的關系才能正確解答此題.


 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案 激活思維優加課堂系列答案
激活思維優加課堂系列答案科目:高中數學 來源: 題型:
【題目】某高校學生總數為8000人,其中一年級1600人,二年級3200人,三年級2000人,四年級1200人.為了完成一項調查,決定采用分層抽樣的方法,從中抽取容量為400的樣本.
(1)各個年級分別抽取了多少人?
(2)若高校教職工有505人,需要抽取50個樣本,你會采用哪種抽樣方法,請寫出具體抽樣過程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a2= ![]() ,且an+1=3an﹣1(n∈N*).
,且an+1=3an﹣1(n∈N*).
(1)求數列{an}的通項公式以及數列{an}的前n項和Sn的表達式;
(2)若不等式 ![]() ≤m對n∈N*恒成立,求實數m的取值范圍.
≤m對n∈N*恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了得到函數 ![]() 的圖象,只需把y=3sin2x上的所有的點( )
的圖象,只需把y=3sin2x上的所有的點( )
A.向左平行移動 ![]() 長度單位
長度單位
B.向右平行移動 ![]() 長度單位
長度單位
C.向右平行移動 ![]() 長度單位
長度單位
D.向左平行移動 ![]() 長度單位
長度單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,a1=2,an+1=4an﹣3n+1,n∈N*(Ⅰ)證明:數列{an﹣n}是等比數列
(Ⅱ)記數列{an}的前n項和為Sn , 求證:Sn+1≤4Sn , 對任意n∈N*成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線 ![]() =1(a>0,b>0)的離心率為
=1(a>0,b>0)的離心率為 ![]() ,過左焦點F1(﹣c,0)作圓x2+y2=a2的切線,切點為E,延長F1E交拋物線y2=4cx于P,Q兩點,則|PE|+|QE|的值為( )
,過左焦點F1(﹣c,0)作圓x2+y2=a2的切線,切點為E,延長F1E交拋物線y2=4cx于P,Q兩點,則|PE|+|QE|的值為( )
A.![]()
B.10a
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個勻速旋轉的摩天輪每12分鐘轉一周,最低點距地面2米,最高點距地面18米,P是摩天輪輪周上一定點,從P在最低點時開始計時,則16分鐘后P點距地面的高度是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(理)如圖,在正方體ABCD﹣A1B1C1D1中,點O為線段BD的中點.設點P在線段CC1上,直線OP與平面A1BD所成的角為α,則sinα的取值范圍是( ) 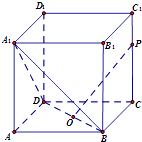
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1]
,1]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com